八年级（上）期末数学练习题

八年级（上）期末数学练习题

班别：　　　　　姓名：　　　　　  　 成绩：　　　　　　  

一、选择题 (共15小题，每小题3分，共45分．)

1.下列计算正确的是　　(　　)

　 A．(ab⁴)⁴＝a⁴b⁸　 B．(a²)³÷(a³)²＝0;  C.　(－x)⁶÷(－x³)＝－x³　 D. －x²y³×10⁰＝0

2．下列各式可以分解因式的是　　(　　)

　　A．x²－(－y²)　　D．4x²＋2xy＋y²　　C　－x²＋4y²　  D．x²－2xy－y²

3．如下图所示，一辆客车从甲站驶往乙站，中途休息了一段时间．如果用横轴表示时间t，纵轴表示客车行驶的路程s，那么下列四个图中较好地反映了s与t之间的函数关系的是 (　　)

　　　

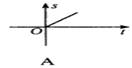
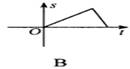
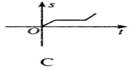
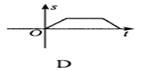
4．下列各式成立的是（　）

　　A．a-b+c=a-（b+c）　　B．a+b-c=a-（b-c）　　C．a-b-c=a-（b+c）　　 D．a-b+c-d=（a+c）-（b-d）

5．下面是一组按规律排列的数：1，2，4，8，16，……，则第2005个数是（　）

　　A．2²⁰⁰⁵　　　 B．2²⁰⁰⁴　　　 C．2²⁰⁰⁶　　　 D．2²⁰⁰³

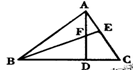
6．如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与EF交于F，BF=AC，那么∠ABC等于（　）

A．45°　　 B．48°　　 C．50°　　 D．60°

(第6题图)　　　　　　　　 (第7题图)

7．在边长为a的正方形中挖掉一个边长为b的小正方形(a>b)，把余下的部分剪拼成一个矩形(如图)．

通过计算图形(阴影部分)的面积，验证了一个等式，则这个等式是(　　)

　A．a²一b²＝(a＋b)(a—b)  B．(a＋b)²＝a²＋2ab＋b² C．(a—b)²＝a²－2ab＋b²  D．a²－ab＝a(a—b)

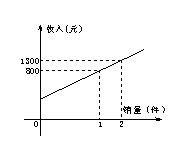8．某公司市场营销部的个人月收入与其每月的销售量成一次函数关系，其图象如图所示，由图中给出的信息可知，营销人员没有销售时的收入是(　　)

A.310元　  B．300元　　C.290元　　D．280元

9．已知x²+kxy+64y²是一个完全式，则k的值是（　）　 (第8题图)

　　A．8　　　B．±8　　　C．16　　  D．±16

10．下列式子中，从左到右的变形是因式分解的是(　　)．

A．(x－1)(x－2)＝x²－3x＋2　　B．x²－3x＋2＝(x－1)(x－2)

C．x²＋4x＋4＝x(x一4)＋4　　D．x²＋y²＝(x＋y)(x—y)

11．直线y=kx+2过点（-1，0），则k的值是（　）

　　A．2　　　B．-2　　　 C．-1　　  D．1

12．若2a^3xb^y＋5与5a^2－4yb^2x是同类项，则(　　)

A、　B、　　　C、　　　　　　D、

13．和三角形三个顶点的距离相等的点是（  ）　　　　　　　　　　　 

A．三条角平分线的交点　　　B．三边中线的交点　　　　　　　　　　 (第14题图)

C．三边上高所在直线的交点　D．三边的垂直平分线的交点 　　　　 

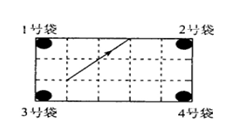
14．如图，是一个改造后的台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔，如果一个球按图中所示的方向被击中(球可以经过多次反射)，那么该球最后将落入的球袋是 (　　)

A．1号袋　　B．2号袋　　C．3号袋　　D．4号袋

15．已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小，则一次函数y=x＋k的图象大致是(　　)．

　　 　 

二、填空题 (每题3分，共30分)

1．计算(－3a³)²·(－2a²)³＝_______

2．填空：x²＋(　　　)＋16＝(　　)²； ( 　　　　　)(－2x＋3y)＝9y²—4x²

3．在扇形统计图中，有两个扇形的圆心角度数之比为3∶4，且知较小扇形

表示24本课外书，那么较大扇形表示_______本课外书．

4．已知△ABC≌△DEF，若∠A=60°，∠F=90°，DE=6cm，则AC=________．

5．若点P(a，b)在第二象限内，则直线y＝ax＋b不经过第_____限．

6．点P关于x轴对称的点是（3，-4），则点P关于y轴对称的点的坐标是_______．

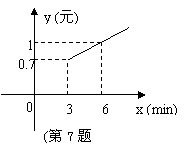
7．在某公用电话亭打电话时，需付电话费y（元）与通话时间x（min）之间的函数关系用图象表示为直线，小文打了2分钟需付费__________元；小文打了8分钟付费__________元。

8．已知a²+b²=13，ab=6，则a+b的值是________．

9．如果A(－1，2)，B(2，－1)，C(m，m)三点在同一条直线上，则m的值等于______．　　　　

10．观察下列各式：(x－1)(x＋1)＝x²－1；(x－1)(x²＋x＋1)＝x³－1；(x－1)(x³＋x²＋x＋1)＝x⁴－1；根据规律(x－1)(xⁿ＋x^n－1＋…＋x＋1)＝____________．

三、解答题(共52分)

1．(8分)计算：(2a－3b)²－(3b＋2a)²，(a²＋ab＋b²)(a²－ab＋b²)．

2．(8分)因式分解： (1)x²－xy－12y²；　　　　　　 (2) a²－6a＋9－b²．

3．（5分）先化简再求值：[（x+2y）（x-2y）-（x+4y）²]÷（4y），其中x=5，y=2．

4．(5分)已知，如图，点B、F、C、E在同一直线上，FB＝CE，AB∥ED，AC∥FD．

　  求证：AB＝ED，AC＝DF．

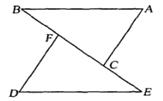
5．(7分)已知，如图，等边△ABC中，D为AC的中点，CE为BC的延长线，且CE＝CD．

　  求证：BD＝DE．

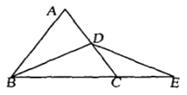
6．(5分)某校500名男生参加体育中考立定跳远测试，将所得成绩整理后分成五组，画出部分频率分布直方图，已知图中从左到右前四个小组的频率依次是0.04,0.24，0.28，0.28．

　  (1)求第五小组的频率，并补全频率分布直方图；

　  (2)若规定2.165m以上为满分，试问该校男生立定跳远得满分的人数有多少?

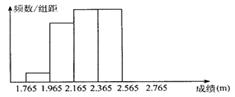
7．(7分)如图，点E在△ABC外部，点D在边BC上，DE交AC于F．若∠1＝∠2＝∠3，AC＝AE，请说明△ABC≌△ADE的道理．

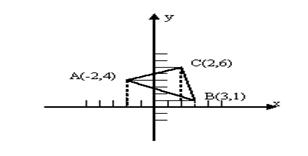
8（5分）在坐标系内画出ΔABC关于y轴对称的ΔA’B’C’并写出三个顶点A’、B’、C’的坐标。

9（5分）．已知：线段a，∠α。求作：等腰三角形ABC，使其腰长AB为a、底角∠B为∠α，

　  要求：用尺规作图，不写作法和证明，但要清楚地保留作图痕迹．

10. （5分）如图，要在河边修建一个水泵站，分别向张庄、李庄送水，修在河边什么地方，可使所用的水管最短？（请通过你所学的知识找出这个地点的位置）

　　　　　　　　　　　　　　　　　　　　　 

11.（10分）在40块同样大小的试验田中，某特种大豆的产量如下：（单位：）

76　115　62　90　107　94　123　103　70　56　136　95　68　118　78　141　78　79　94　105　100　64　72　100　97　131　62　132　123　58　87　70　 107　79　52　94　80　 81　50　72

（1）最大值与最小值的差。 （2）决定组距与组数。　（3）列出频数表。　（4）绘出频数分布直方图。

　

　

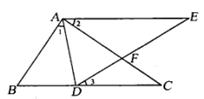
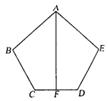12．（5分）已知：如图，AB＝AE，BC＝ED，AF是CD的垂直平分线，

求证：∠B＝∠E．

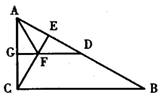
13．（8分）如图，在△ABC中，∠ACB=90°，CE⊥AB于点E，AD=AC，AF平分∠CAB交CE于点F，DF的延长线交AC于点G，求证：（1）DF∥BC；（2）FG=FE.

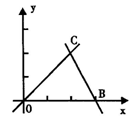
14．（12分）如图，直线OC、BC的函数关系式分别是y₁=x和y₂=-2x+6，动点P（x，0）在OB上运动（0<x<3），过点P作直线m与x轴垂直．

　（1）求点C的坐标，并回答当x取何值时y₁>y₂？

　（2）设△COB中位于直线m左侧部分的面积为s，求出s与x之间函数关系式．

15．（5分）为了保护学生的视力，课桌的高度)ycm与椅子的高度xcm(不含靠背)都是按y是x的一次函数关系配套设计的，下表列出了两套课桌椅的高度：

	第一套	第二套
椅子高度xcm	40.0	37.0
课桌高度ycm	75.0	70.2

 (1)请确定)y与x的函数关系式(不要求写出x的取值范围)；

(2)现有一把高42.0cm的椅子和一张高78.2cm的课桌，它们是否配　　 套?请通过计算说明理由。

16．（5分）（10分）某批发商欲将一批海产品由A地运往B地，汽车货运公司和铁路货运公司均开办了海产品运输业务．已知运输路程为120千米，汽车和火车的速度分别为60千米/时和100千米/时．两货物公司的收费项目和收费标准如下表所示：

运输工具	运输费单价（元/吨·千米）	冷藏费单价（元/吨·小时）	过路费（元）	装卸及管理费（元）
汽车	2	5	200	0
火车	1.8	5	0	1600

　　注：“元/吨·千米”表示每吨货物每千米的运费；“元/吨小时”表示每吨货物每小时的冷藏费．

　　（1）设该批发商待运的海产品有x（吨），汽车货运公司和铁路货运公司所要收取的费用分别为y₁（元）和y₂（元），试求出y₁和y₂和与x的函数关系式；

（2）若该批发商待运的海产品不少于30吨，为节省运费，他应该选择哪个货运公司承担运输业务？