八年级（下）半期考试数学试卷
A卷 满分100分
一、填空题（每空格2分，共30分）
1、不等式x－4＜0的解集是_________；不等式－2x＜－1的解集是________.
2、x的3倍与8的和比x 的5倍大，用符号表示为_______________.
3、已知a>b，用“>” 或“<”号填空：
⑴－a______－b； ⑵ a－b______0; ⑶ 3－2a______3－2b.
4、当a=_______时，分式
没有意义。
5、当x______时，代数式2x－3的值不小于零.
6、在横线上填上适当的式子，使得等式成立：
.
7、计算：
____________.
8、已知ab=6，a+b=5，则多项式ab2+ab2的值为_____________.
9、若不等式组
无解，则m的取值范围是____________.
10、已知ab<0，bc>0则函数
的图像不经过第
象限
11 甲做90个零件所需要的时间和乙做120个零件所用的时间相同，又知每小时甲、乙两人共做35个机器零件。设甲每小时做x个零件.
则可得方程：__________________________.
12 甲、乙两组学生去距学校4.5千米的敬老院打扫卫生，甲组学生步行出发半小时后，乙组学生骑自行车开始出发，结果两组学生同时到达敬老院，如果步行的速度是骑自行车的速度的3倍， 
设步行的速度是x千米/小时.
则可得方程：__________________________.
二、选择题（每题3分，共15分）
13、下列判断中，正确的是（ ）
A、分式的分子中一定含有字母 B、分数一定是分式
C、当A=0时，分式
的值为0（A、B为整式） D、当B=0时，分式无意义
14、计算
的结果是（ ）
A、
B、－22007 C、22007 D、2
15、若把分式
中的x和y都扩大3倍，那么分式的值（ ）
A、扩大3倍 B、不变 C、缩小3倍 D、缩小6倍
16、下列各式从左到右，是因式分解的是（ ）
A、（y－1）（y＋1）＝
－1
B、
C、（x－2）（x－3）＝（3－x）（2－x） D、
17、小明在抄分解因式的题目时，不小心漏抄了x的指数，他只知道该数为不大于10的正整数，并且能利用平方差公式分解因式，他抄在作业本上的式子是
□－
（“□”表示漏抄的指数），则这个指数可能的结果共有 （ ）
A、2种 B、3种 C、4种 D、5种
三、解下列不等式（组）（每题4分，共8分）
18、解不等式3x－1＜2x＋1，并把它的解集在数轴上表示出来。
 | |||||
 | | ||||
19、解下列不等式组
，并把它的解集在数轴上表示出来。
 |
四把下列各式分解因式（每题5分，共20分）
20、
21、
22、
；
23、 
；
五、.计算与化简（每题5分，共10分）
24计算
25化简求值
其中x=
六、解答题（共17分）
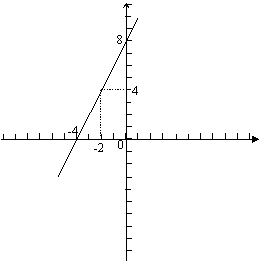
26、(4分)、已知函数y=2x+8的图象，根据图象回答下列问题：
⑴当x_________值时，y＞0.
⑵当x_________值时，y＞8.
⑶当－2≤x≤0时，则相应y的取值范围
是___________.
⑷如果这个函数y的值满足0≤y≤4，
则相应的x的取值范围是__________.
27、(6分)、已知一次函数
的图象与x轴的交点在A（－1,0）与B（5,0）之间（包括A、B两点），求m的取值范围。
28（7分）、某超市规定：凡一次购买某种大米180kg以上可以按原价打折出售，购买180kg（包括180kg）以下只能按原价出售。小明到这家超市买该种大米，按原计划买大米，只能按原价付款，需要500元；若比计划多买40kg，则按打折价格付款，恰巧需要也是500元。
⑴求小明原计划购买大米数量x（千克）的范围；（2分）
⑵若按原价购买4kg与打折价购买5kg的款相同，那么原计划小明购买多少大米？（5分）
B卷满分50分
一、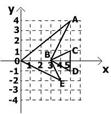
选择题（每题5分共20分）
1、平面直角坐标系中，有一条“鱼，它有六个顶点”，则（ ）
A.将各点横坐标乘以2，纵坐标不变，得到的鱼与原来的鱼位似
B.将各点横、纵坐标都乘以2，得到的鱼与原来的鱼位似
C.将各点纵坐标乘以2，横坐标不变，得到的鱼与原来的鱼位似
D.将各点横坐标乘以2，纵坐标乘以
，得到的鱼与原来的鱼位似
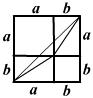2、观察图形，判断(a2+b2)与2
的大小（ ）
A.(a2+b2)＞2
B.(a2+b2)＜2
C.(a2+b2)≤2
D.(a2+b2)≥2
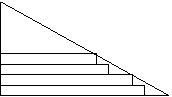
3、某班在布置新年联欢晚会会场时，需要将直角三角形彩纸裁成长度不等的矩形彩条。如图在
，依次裁下宽为1cm的纸条，若使裁得的矩形纸条的长都不小于5cm，则每张直角三角形彩纸能裁成的矩形纸条总数是（
）
A 24
B 25
C 26 D 27
|
|
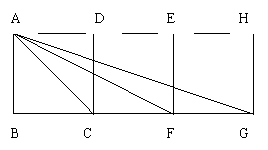
4、如图，四边形ABCD，DCFE，EFGH是三个边长为a的正方形，小明发现∠1＋∠2＝ 度。
A.、45 B、 37.5 C、60 D、 40
二、 解方程 （每题5分共10分）
5、
6、 
三、解答题（共20分）
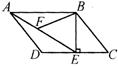7、（6分）如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE．F为AE上一点，且∠BFE＝∠C．
(1)求证：△ABF∽△EAD；
(2)若AB＝4，∠BAE＝30°，求AE的长；
(3)在（1）、（2）的条件下，若AD＝3，求BF的长．（计算结果可含根号）
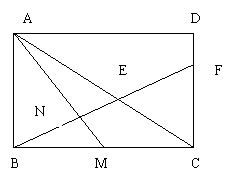
8、(7分)如图,平行四边形ABCD中，M为BC的中点，AN＝3NM,BN的延长线交AC于E，交CD于F，(1)求AE：EC的值。（2）当S△ABC＝9时，求S△ECF.
 |
9、（7分）某企业有员工300人，生产A种产品，平均每人每年可创造利润m万元（m为大于零的常数）。为减员增效，决定从中调配x人去生产新开发的B种产品。根据评估，调配后，继续生产A种产品的员工平均每人每年创造的利润可增加20%，生产B种产品的员工平均每人每年可创造利润1.54m万元。
（1）调配后，企业生产A种产品的年利润为 万元，企业生产B种产品的年利润为 万元（用含x和m的代数式表示）。若设调配后企业全年总利润为y万元，则y关于x的函数解析式为 。
（2）若要求调配后，企业生产A种产品的年利润不小于调配前企业年利润的
，生产B种产品的年利润大于调配前企业年利润的，应有哪几种调配方案？请设计出来，并指出其中哪种方案全年总利润最大（必要时，运算过程可保留3个有效数字）。