13.3角平分线的性质(二)
【基础知识扫描】
1.点O是△ABC内一点,且点O到三边的距离相等,∠A=60°,则∠BOC的度数为( )
A.60°B.90°C.120°D.150°
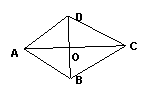
2.如图,AB=AD,CB=CD,AC、BD相交于点O,则下列结论正确的是( )
A. OA=OC B. 点O到AB、CD的距离相等
C. 点O到CB、CD的距离相等 D. ∠BDA=∠BDC 第2题图
3.△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D,OE⊥AC于E,
OF⊥AB于F,且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( )
A.2cm 2cm 2cm B. 3cm 3cm 3cm C. 4cm 4cm 4cm D. 2cm 3cm 5cm
4.到一个角的两边距离相等的点在 ;角平分线上的点到这个角的两边的距离
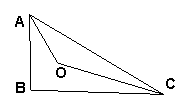5.如图,△ABC中,∠B=90°, ∠A、∠C的平分线交于点O，则∠AOC的度数为
 | |||
 | |||
第5题图 第6题图 第7题图
【能力训练升级】
6.如图,P是∠AOB的平分线上的一点,PE⊥OA于E,PF⊥OB于F,OP与EF的位置关系是
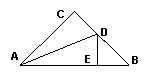
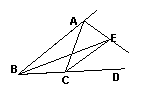7.如图，在△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于点D，DE⊥AB，垂足为E，且AB=6cm，则△DEB的周长为__ cm.
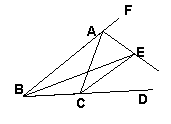
8.如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于E,求证:AE平分∠FAC
第8题图
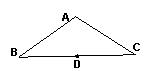
9.如图,已知△ABC中,AB=AC,D是BC的中点,求证:D到AB、AC的距离相等.
第9题图
【探究创新实践】
10.如图,已知AB=AC,AD=AE,DB与CE相交于O,(1)若DB⊥AC于D,CE⊥AB于E,试判断OE与OD的大小关系.并证明你的结论.(2)若没有第（1）中的条件,是否有这样的结论?试说明理由.
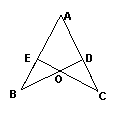
第10题图
13.3角平分线的性质(二)答案
1．C 2.C 3.A 4.这个角的平分线上；相等； 5. 135 ° 6.垂直 7. 6 8. 过点E分别作EF⊥BD、EG⊥BA、EH⊥AC，垂足分别为F、G、H，∵BE平分∠ABC,∴EF=EG，∵CE平分∠ACD，∴EF=EH，∴ EG=EH，∴AE平分∠FAC 9. 连接AD，∵ D为BC的中点，∴BD=DC，又∵AB=AC，AD=AD，
∴ △ABD≌△ACD ，∴∠BAD=∠CAD，∴D到AB、AC的距离相等； 10. （1）OD=OE，证明略（2）成立，证明略