八年级数学第二学期阶段教学质量检测
试题卷
一.选择题：(每小题3分,共30分)
1.若
有意义,则( )
A.
B. 
C. 
D.
2.下列方程
，配方正确的是（ ）
A.
B.
C. 
D.
3.一个容量为80的样本，最大值是141 ，最小值是50，取组距为10，可分成（ ）组
A.10组 B.9组 C. 8组 D.7组
4.一棵大树在一次强台风中离地5米处折断,倒下部分与地面成30°夹角,这棵大树在折断前的高度是( )
A.10米 B.15米 C.25米 D.30米
5.平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m, 则m的取值范围是（ ）
A.1<m<11 B.2<m<22 C. 10<m<12 D. 5<m<6
6.下列定理有逆定理的是（ ）
A.直角都相等
B. 若
，则
C.末位数是2的整数被2整除 D. 直角三角形的两锐角互余
7. 已知：关于x的一元二次方程
，则m的取值是（ ）
A.±3 B.3 C.-3 D.2
8.若铺地面的地砖绕一点处由3块相同的正多边形组成,则这个正多边形是( )
A.正三角形 B.正六边形 C.正方形 D.正五边形
9.如图;已知长方形ABCD中,P,R是CB,CD上的动点,E,F是AP,RP的中点,当P在BC上从B向C移动而R在CD上从C向D移动时,那么下列结论成立的是( )
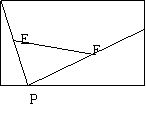A . 线段EF的长逐渐增大 A D
B. 线段EF的长逐渐减小
C. 线段EF的长不变 R
D. 线段EF的长不能确定
B C
10.用反证法证明:“在△ABC中,至多有一个锐角或钝角” ,第一步应假设( )
A.三角形中至少有一个直角或钝角
B. 三角形中至少有两个直角或钝角
C. 三角形中至少有三个直角或钝角
D. 三角形中三个角都是直角或钝角
二.填空题:(每小题4分,共24分)
11.方程
的解为
12. 写出命题“对顶角相等”的题设
13.长方形木板锯掉一个角后,剩下的多边形的内角和是
14.若二次根式
的值为整数,则整数m的值是
15.已知:
,那么
=
16.下列命题 ①有两边和其中一边的对角相等的两个三角形全等 ②三角形的内角至少有一个不小于60°③若 a,b,c是三角形的三条边，则
④8点30分，时针与分针的夹角是60° ⑤若n是自然数，则
不可能为3的倍数,上述命题是真命题的是
三.解答题：（第17，18，19题各6分，第20，21题各8分，第22，23题各10分，第24题12分）
17.计算(每小题3分,共6分)
①
② 
18. 解方程(每小题3分,共6分)
① 
② 
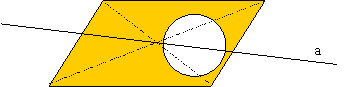
19.(6分)如图:平行四边形内有一个圆,请画出一条直线,将阴影部分的面积平分
(要求保留作图痕迹,不要求证明)
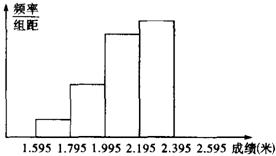
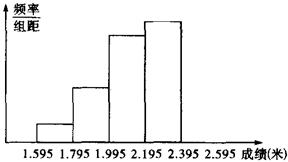
20．(8分)为增强学生的身体素质，某校坚持长年的全员体育锻炼，并定期进行体能测试．下图是将某班学生的立定跳远成绩(精确到0.01米)进行整理后，分成5组，画出的频率分布直方图的一部分，已知从左到右4个小组的频率分别是0.05，0.15，0.30，0.35，第5小组的频数是9．
(1)请将频率分布直方图补充完整；
(2)该班参加这次测试的学生有多少人?
(3)若成绩在2.00米以上(含2.00米)的为合格，问该班成绩的合格率是多少?
21. (8分) 阅读材料:并仿造例题解决后面的问题:
化简
解:=
=
(1)化简:
(2)化简:
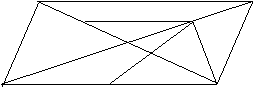
22. （10分）如图：在平行四边形ABCD中，对角线AC，BD相交于点O，BD=2AD，E，F，G分别是OC，OD，AB的中点，求证：（1）BE⊥AC （2）EG=EF
D C
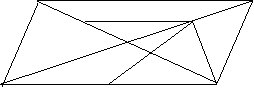F
E
O
A G B
23.（10分）如图:一块长是a米，宽是b米的长方形场地，计划在该场地上修建两条宽是2米且互相垂直的道路，余下的四块场地修成草坪（1）请分别写出每条道路的面积（用含a,b的代数式表示）
（2）若a:b=2：1，并且四块草坪的面积和是312平方米，试计算出长方形的长与宽分别是多少米？
24.(12分) 如图:△ABC是等边三角形,点D,E,F分别在AB,BC,CA上
①若AD=BE=CF,问△DEF为等边三角形吗?试证明你的结论。
②若△DEF为等边三角形, 问AD=BE=CF成立吗? 试证明你的结论。
A
F
D
B E C
2八年级数学第二学期阶段教学质量检测答题卷
一.选择题：(每小题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二.填空题:(每小题4分,共24分)
11. 12.
13. 14.
15.
16.
三.解答题：（第17，18，19题各6分，第20，21题各8分，第22，23题各10分，第24题12分）
17.计算(每小题3分,共6分)
①
②
18. 解方程(每小题3分,共6分)
① ②
19.(6分)
20．(8分)
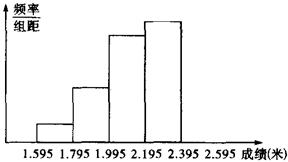
(1)
(2)
(3)
21.（8分） 阅读材料:并仿造例题解决后面的问题:
(1)化简:
(2)化简:
22 (10分)
D C
F E
O
A G B
（1）
（2）
23.（10分）
（1）
（2）
24.(12分)
A (1)
F
(2)
D
B E C
八年级数学第二学期阶段教学质量检测参考答案
一.选择题：(每小题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | A | B | A | D | C | B | B | B |
二.填空题:(每小题4分,共24分)
11. 
12. 如果两个角是对顶角
13. 180°，360°，540°（答对一个2分，答对2个3分，答错不得分）
14. m= -1 15..
16. ②③⑤
（答对一个2分，答对2个3分，答错不得分）
三.解答题：（第17，18，19题各6分，第20，21题各8分，第22，23题各10分，第24题12分）
17.计算(每小题3分,共6分)
①
②
=
=
18. 解方程(每小题3分,共6分)
① ②
19.(6分)
∴直线a即所求平分阴影部分面积的直线
(作图5分，结论1分)
20．(8分)
(1)2分
(2)
3分
(3)80﹪ 3分
21.（8分）
阅读材料:并仿造例题解决后面的问题:
(1)
（4分）
(2)
（4分）
22.(10分)
D
C
F E
O
A G B
（1）∵平行四边形ABCD，对角线相交于O点
∴AD=BC DB=2BO AB=CD（2分） 又因为BD=2AD
∴BO=BC，（2分） 又因为E是CO的中点，∴BE⊥AC（等腰三角形三线合一）（1分）
（2）∵BE⊥AC 所以△AEB是直角三角形，且G是AB中点
∴EG=
AB （2分）
又因为E，F是OC，OD的中点，所以EF=DC，且AB=DC (2分)
∴EG=EF （1分）
23.（10分）
（1）2a米2,2b米2 （4分）
（2）解：设宽是x米 ,长是2x米 1分
则草坪面积和是 
，
由条件得方程=312
2分
解得x1=14 x2=-11 (舍) 长是28米 2分
答：长方形的长是28米，宽是14米。 1分
24.(12分)
A
(1)∵△ABC是等边三角形
∴AB=BC=CD ∠A=∠B=∠C （1分）
F 又∵AD=BE=CF
D ∴BD=CE=AF （1分）
∴△ADF≌△BED≌△CFE （SAS）2分
B E C ∴DE=DF=EF △DEF是等边三角形 2分
（2）∵△DEF 与△ABC 是等边三角形
∴∠B=∠C=∠DEF=60° DE=EF,∴∠DEB+∠FEC=∠FEC+∠EFC=120°
∴∠DEB=∠EFC （2分）
在△DEB 与△EFC中
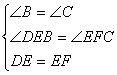
∴△DEB≌△EFC （AAS） 2分 ∴ BE=FC 1分
同理△FDA≌△DEB AD=EB ∴AD=BE=CF 1分