八年级数学第二学期期末考试卷

八年级数学第二学期期末考试卷

（满分150分，时间120分钟）

一、　　　　　 填空（4分×11=44分）

1．的算术平方根为___________，的立方根为___________。

2．化简：__________，___________。

3．已知两个相似三角形的面积比为9：4，则它们的相似比为___________，其中一个周长为36，则另一个周长为___________。

4．函数的自变量的取值范围是___________。

5．在比例尺1：10000的地图上，相距40cm的两地实际距离为__________千米。

6．已知，则=　___________。

7．已知：的面积为。如果BC边的长为，这边上的高为，那么 之间的函数关系式为______________________。

8．如果反比例函数的图象在二、四象限，则=______________。

9．升国旗时，某同学站在离旗杆底部24米处行注目礼，当国旗升至旗杆顶端时，该同学的视线的倾角恰好为30º，若双眼离地面1.5米，则旗杆高度为_________米。（用含根号式子表示）

10．如图，若，则此图中有_________组相似三角形。

11．如图，已知AD是斜边BC上的高，且AB=6，BC=10。则AC= _________，=_____________。

　　　　　 A　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　A

　　　　　　　　 1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

 E　　　　　　　　　　　 D

2

C　　　　　　　　　　　　　　　　　 B　　　　　　　　　　　　　　B　　　　　　　D　　　　　　　　　　　　　C

　　　　　　（10题 ）　　　　　　　　　　　　　　　　　　　　　　　　　（11题）

二、　　　　　 选择题（4分×9=36分）

12．下列各式中，最简二次根式是（　　）

（A）　（B）　（C）　（D）

13．下列各式的计算中，成立的是（　　）

（A）　　　　　　　 （B）

（C）　　　　　　 （D）

14．式子的值为（　　）

（A）　 正数　（B）非正数  （C）非负数　（D）负数

15．在中，已知，则下列比例式中成立的是（　　）

（A）（B）　　　　　　　　　　　　　　　　　　　　　　　 A

（C）（D）　　　　　　　　　　　　　　　 M　　　　　　　　　 N

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 1

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B　　　　　　　　　　　　　　　　　　　　　　C

16．根据下列条件，能判断的是（　　）

（A）

（B）

（C）

（D）

17．下列函数中，在全体实数范围内，随的增大而增大的是（　　）

（A）（B）（C）（D）

18．一次函数的图象与坐标轴交于A、B两点，A、B两点间

的距离为（　  ）

（A）（B）（C）（D）

19．已知：中，，下列关系式中成立的式子共有（　　）

①；　　　　②；

③：　　　　④。

（A）1个　  （B）2个　 （C）3个　　（D）4个

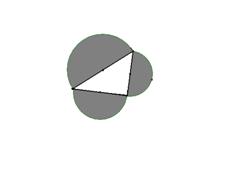
20．如图，分别以三角形三边为直径向外作三个半圆，如果较小的两个半圆面积之和等于较大的半圆面积，则这个三角形为（　　）

（A）　 锐角三角形（B）钝角三角形

（C）直角三角形（D）锐角三角形或钝角三角形

 

　　　　　　　　　　　　　　　　　　　　 　　　

三、　　　　　 解答题（7分×6=42分）

21．计算：

22．计算：

23．计算：

24．在中，，求边及、的度数。

25．如图四边形CDEF是的内接正方形，AC=4，BC=6，求ED的长。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 A

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　E　　　　　　　 D

B　　　　  F

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　C

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

26．如图，已知，则与相似吗？为什么？

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 A

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1　　　2　　　　　E

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 3

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 C

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B　　　　　　　　 D

四、做图题（6分×2分=12分）

27．在下列网格中，画四边形DEFG，使四边形DEFG∽四边形ABCD，且相似比不为1。

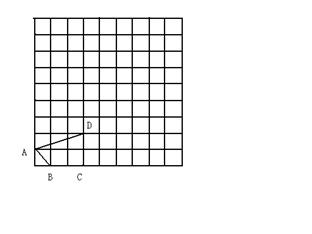
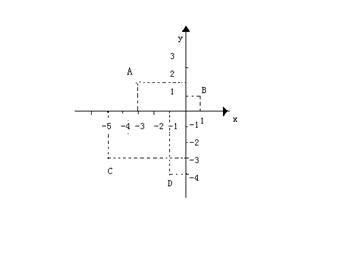
28．如图，学校有四栋学生宿舍，分别用A、B、C、D表示，建立如图所示的直角坐标系，四地的坐标分别为A（）、B（1，1）、C（）、D（）。为了方便学生，学校要新建一个食堂，你认为新建食堂修在哪里，对大家都方便？在图上指出食堂的具体位置和坐标。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

五、解答题（8分×2=16分）

29．如图，一个正比例函数的图象和一个一次函数的图象交于点A（—1，2），且的面积为5，求这两个函数的解析式。　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 A　　　　　　2

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　1

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B　 —1　　　　　　　　　　

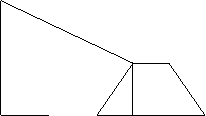
30．城市规划期间，欲拆除一电线杆AB，已知距电线杆AB水平距离14米的D 处有一大坝，背水坡CD的高度i =2：1，坝高CF=2米，在坝顶C处测得杆顶A的倾角为30º，DE之间是宽为2米的人行道，试问：在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封上？试说明理由。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　A

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　30º　　　　C

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 人

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B　　　　　　　　　　　　　　行

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　E　　　　 道D　  F  

重庆市北碚区兼善中学第二学期数学期末考试

1．3，4  2．　3．3：2，24或54  4． 5．4  6．

7．　 8．　9．　10．3　11．8，

12B  13D　14D　15B　16D  17D　18A　19C　20C

21．原式

　　　　

22．原式

　　　　

23．原式

　　　　

　　　　

24．在中，，

因为所以。

又因为，所以

25．因为四边形CDEF是正方形，所以ED//BC，

所以

设ED=，而AC=4，BC=6

则即ED=2.4

26．与相似

　 因为，所以

　 又因为，所以

　 所以∽

27．略

28．提示：作AD与BC的交点，坐标为

29．①设因为

所以，所以

②设

因为

，所以点B（—5，0）

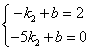
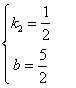所以所以

30．过点C作CM⊥AB，垂足为M，可得：

①DF=1，②MC=15，③AM=，④AB=

因为BE=12

所以AB<BE

所以此人行道不必封上