八年级数学第三、四章复习题
一、选择题 姓名
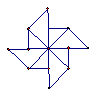
1.下列图形中，绕某个点旋转
能与自身重合的有（ ）
①正方形 ②长方形 ③等边三角形 ④线段 ⑤角 ⑥平行四边形
A. 5个 B. 2个 C. 3个 D. 4个
2.图案（A）-（D）中能够通过平移图案（1）得到的是（ ）.
（1） （A） （B） （C） （D）
3.下列说法不正确的是（ ）
A.中心对称图形一定是旋转对称图形 B、轴对称图形一定是中心对称图形
C、在成中心对称的两个图形中，连结对称点的线段都被对称中心平分
D、在平移过程中，对应点所连的线段也可能在一条直线上
4.如图3，图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
A、300 B、600 C、900 D、1200
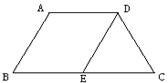
5.如图4，面积为12cm2的△ABC沿BC方向平移至△DEF的位置，平移的距离是边BC长的两倍，则图中的四边形ACED的面积为（ ）
A、24cm2 B、36cm2 C、48cm2 D、无法确定
6.如图5，在正方形ABCD中，E为DC边上的点，连结BE，将△BCE绕点C顺时针方向旋转900得到△DCF，连结EF，若∠BEC=600，则∠EFD的度数为（ ）
A、100 B、150 C、200 D、250
图3 图4 图5
14.在以下现象中，
① 温度计中，液柱的上升或下降； ②
打气筒打气时，活塞的运动；
③ 钟摆的摆动； ④
传送带上，瓶装饮料的移动
属于平移的是（ ）
（A）① ，② （B）①， ③ （C）②， ③ （D）② ，④
7.从8:55到9:15,钟表的分针转动的角度是 ，时针转动的角度是 。（ ）
A. 120 0、10 0 B. 30 0、 15 0 C. 12 0、60 0 D. 10 0、120 0
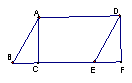
8．如图，等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，△DEC的周长是 （ ）
A、3 B、12
C、15 D、19
9．四边形ABCD的对角线AC和BD相交于点O，设有下列条件：①AB=AD；②∠ DAB=900；③AO=CO，BO=DO；④矩形ABCD；⑤菱形ABCD，⑥正方形ABCD，则在下列推理不成立的是 ( )
A、①④
⑥ B、①③⑤ C、①②⑥ D、②③④
10．下列美丽的图案，既是轴对称图形又是中心对称图形的个数是
 |
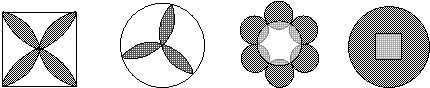11．如果要用正三角形和正方形两种图形进行密铺，那么至少需要（ ）
A 三个正三角形，两个正方形 B 两个正三角形，三个正方形
C 两个正三角形，两个正方形 D 三个正三角形，三个正方形
12．下列命题中，正确命题是（ ）
A．两条对角线相等的四边形是平行四边形；
B．两条对角线相等且互相垂直的四边形是矩形；
C．两条对角线互相垂直平分的四边形是菱形；
D．两条对角线平分且相等的四边形是正方形。
13．观察下面的图形的规律，虚线框内应填入的是
|  | |||
 | |||
 | |||
14．如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带( )去配..
A.① B.② C.③ D.①和②
15．将一圆形纸片对折后再对折，得到图3，然后沿着图中的虚线剪开，
得到两部分，其中一部分展开后的平面图形是( )
二、填空题：
1.图（1）绕着中心最小旋转 能与自身重合。
2.将任意一个三角形绕着其中一边的中点旋转，
所得图形与原图形可拼成一个 。
3.等边三角形至少旋转__________度才能与自身重合。
4．如图，△ABC绕点B逆时针方向旋转到△EBD的位置，若∠A=150，
∠C=100，E，B，C在同一直线上，则∠ABC=________，旋转角度是__________。
5．如图，矩形ABCD中，AB＝3，BC＝4，如果将该矩形沿对角线BD折叠，那么图中阴影部分的面积是
. 
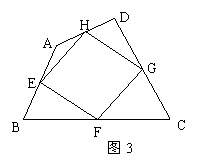
6．如图3，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，请添加一个条件，使四边形EFGH为菱形，并说明理由．
解：添加的条件： 理由：
7．正n边形的内角和等于1080°，那么这个正n边形的边数n=_____.
8．若一个多边形的内角和是外角和的5倍，则这个多边形是 边形；
9．菱形的一个内角是60º，边长是5cm，则这个菱形的较短的对角线长是 cm；
10． 顺次连接一个任意四边形四边的中点，得到一个四边形 .
11．铺成一片可以不留空隙的平面图形有 （写三个）；
三．解答题
1．、已知：在△ABC中，AB=AC=a，M为底边BC上任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q.
(1)求四边形AQMP的周长；
(2)写出图中的两对相似三角形（不需证明）；
(3)M位于BC的什么位置时，四边形AQMP为菱形？说明你的理由.
2、四边形是大家最熟悉的图形之一，我们已经发现了它的许多性质.只要善于观察、乐于探索，我们还会发现更多的结论.
(1)四边形一条对角线上任意一点与另外两个顶点的连线，将四边形分成四个三角形(如图①)，其中相对的两对三角形的面积之积相等.你能证明这个结论吗？试试看.
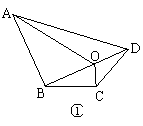已知：在四边形ABCD中，O是对角线BD上任意一点（如图①）；
求证：S△OBC·S△OAD=S△OAB·S△OCD.
证明：
 |
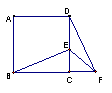
3．如图，菱形ABCD中，E是AD中点，
EF⊥AC交CB的延长线与点F。
（1） DE和BF相等吗？请说明理由。
（2） 连结AF、BE，四边形AFBE是平
行四边形吗？说明理由。
四、作图题：
1．如图，⑴△ABC经过平移后，B点移到了C处，作出平移后的三角形。
[2]请你作出四边形ABCD绕点O顺时针旋转60度后的图形。（6分）
|
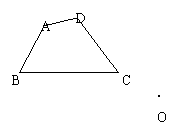
2．.如图,四边形ABCD的∠BAD=∠C=90º,AB=AD,AE⊥BC于E,
旋转后能与
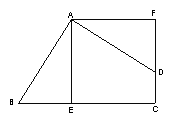
重合。
（1）.旋转中心是哪一点?（2）.旋转了多少度?（3）.若AE=5㎝,求四边形AECF的面积。
3．.利用平移、旋转、轴对称分析下面两个图案的形成过程。
（说出任意一种形成过程即可）
 | |||
 | |||