八年级《数学》（下）单元检测
期末试卷（A卷）
（满分：100分，完卷时间：100分钟）
班级_______ 姓名_______ 得分_______-
一、精心选一选(下列各小题的四个选项中，有且只有一个是符合题意的，把你认为符合题意的答案代号填入答题表中，每小题3分，共24分)
1、在
中分式的个数有（ ）
A、2个 B、3个 C、4个 D、5个
2. 如果点(a，－2a)在双曲线
上，则此双曲线的图象在 ( )
(A)第一、二象限 (B)第一、三象限 (C)第二、四象限 (D)第三、四象限
3. 下列变形中，不正确的是 ( )
(A) 
(B)
(C) 
(D) 
4、某服装销售商在进行市场占有率的调查时，他最应该关注的是（ ）
A. 服装型号的平均数 B. 服装型号的众数 C. 服装型号的中位数 D. 最小的服装型号
5、五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（ ）
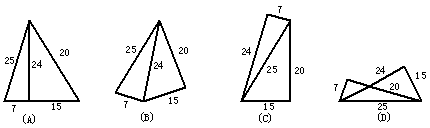
6. .已知在四边形ABCD中，AB∥CD，如果再增加一条件，就能判定该四边形为平行四边形，下面所增加的四个条件正确的是 （ ）
A.∠A=∠B B. BC=AD. C.AC=BD D. BC∥AD
7、某市为处理污水需要铺设一条长为4000米的管道，为了尽量减少施工对交通所造成的影响，实际施工时每天比原计划多铺设10米，结果提前20天完成任务。设原计划每天铺设管道x米，则可得方程（ ）
A、 
B、
C、 
D、 
8. 在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成平行四边形，又能拼成三角形和梯形的是( )
 |
(A) (B) (C) (D)
二、细心填一填(每题3分，共18分)
9．当x_________时，分式
有意义；当x
时，分式
无意义；
10、如果反比例函数的图象经过点（1，-2），那么这个反比例函数的解析式为_______
11、如图，□ABCD中，AE⊥CD于E，∠B=55°，
则∠D= ，∠DAE= 。
12、单位举行歌咏比赛，分两场举行，第一场8名参赛选手的平均成绩为88分，第二场4名参赛选手的平均成绩为94分，那么这12名选手的平均成绩是 分
13、小红和小军周日去郊外放风筝，小军手中的的25米线全放出去了，高兴的小军紧紧地拉着线坐在了草地上，小红想知道风筝究竟有多高，她量了一下高高飞扬的风筝的正下方的地方到小军坐着的地方约为20米，则风筝的高度约为________
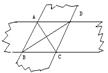
14、 如图所示，将两条等宽的纸条重叠在一起，则四边形ABCD是
，若AB=8，∠ABC=60
，则AC=。
三、耐心算一算、（本大题共3小题，满分20分.）
15、（1）化简：
（2）解分式方程： 
＋
＝3．
16 （10分）请你阅读下列计算过程，再回答所提出的问题：
计算
解：原式=
（A）
=
（B）
=x-3-3(x+1) （C）
=-2x-6 （D）
（1）上述计算过程中，从哪一步开始出现错误：_______________
（2）从B到C是否正确，若不正确，错误的原因是__________________________
（3）请你正确解答。
四.解答下列各题：
17、（8分）、如图，矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F，试说明四边形AFCE是菱形.
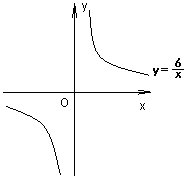18、（10分）若反比例函数
与一次函数
的图象都经过点A（
，2）
（1）求点A的坐标；
（2）求一次函数的解析式；
（3）设O为坐标原点，若两个函数图像的另一个交点为B，
求△AOB的面积。
五.列方程解应用题（本题8分）
19、(8分)为了开发旅游风景区，需要修一条长为1000米的大道，实际施工时每天的工效比原计划增加25%，结果提前10天完成，原计划每天修路多少米？
六. （本题12分）
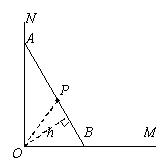
20. 如图所示，一根长2.5米的木棍(AB)，斜靠在与地面（OM）垂直的墙（ON）上，此时OB的距离为0.7米，设木棍的中点为P．若木棍A端沿墙下滑，且B端沿地面向右滑行。
(1)如果木棍的顶端A沿墙下滑0.4米，那么木棍的底端B向外移动多少距离？
(2)请判断木棍滑动的过程中，点P到点O的距离是否变化，并简述理由。
(3)在木棍滑动的过程中，当滑动到什么位置时，△AOB 的面积最大？简述理由，并求出面积的最大值。
期末试卷（A卷）
答案：
1． A 2.C 3.D 4.B 5.C 6.D 7.D 8.D
9.
X≠1 X=－
10. Y=－
11.
55O 35O 12. 90分
13． 15 14. 菱形 15. （1）
（2） x=
16. （1）A到B
（2）不正确，不能去分母
（3）＝
＝
＝
17． 略
18. （1）点A的坐标（3，2）
（2）
（3）△AOB的面积为8。
19. 设原计划每天修路x米，则实际每天修1.25x米
依题意，得
整理得：
∴
经检验知：是原方程的解
答：原计划每天修路20米20.
20. （1）不变。理由：在直角三角形中，斜边上的中线等于斜边的一半，因为斜边AB不变，所以斜边上的中线OP不变。
（2）当△AOB的斜边上的高h等于中线OP时，△AOB的面积最大。
如图，若h与OP不相等，
则总有h<OP。
故根据三角形面积公式，
有h与OP相等时△AOB的面积最大
此时，S△AOB=
.
所以△AOB的最大面积为
。