八年级数学期中考试试卷
班级 姓名 计分
一、选择题（每题3分，共30分）
1、下列函数中，是一次函数的是（ ）
A、y＝-2x2 B、y＝
C、y＝-x+3 D、y＝2x
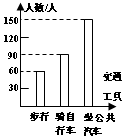
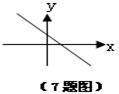
2、如右图所示，下列说法正确的是（ ）
A、步行人最少且为90人;
B、步行人数为50人;
C、坐公共汽车的人数占总数的50%;
D、步行与骑自行车的人数和比坐公共汽车的人数要少.
3、若一次函数y=kx+b的图象经过点（-2,-1）和点（1,2），
则这个函数的图象不经过（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
4、某农场今年粮食、棉花、油料作物种植面积的比是5：2：1，在扇形统计图上表示粮食面积的扇形圆心角是（ ）
A.2200 B.450 C.2250 D.900
5、已知样本：7，10，8，14，9，7，12，10，8，12，10，8，11，10，9，13，11。那么这组样本数据落在8.5——11.5的频数是（ ）
A.8 B.12 C.10 D.13
6、既在直线Y=-3X-2上，又在直线Y=2X+8上的点是（ ）
A.（-2，4） B.（-2，-4）
C.（2，4） D.（2，-4）
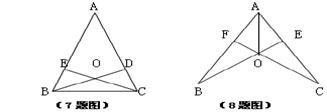
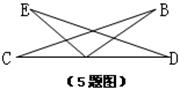
7、如图，已知AB=AC，要使△ABD≌△ACE，只需补充条件（ ）
A、∠BOE=∠COD B、∠DOE=∠BOC C、BE=CD D、BO⊥CO
8、如图，AO平分∠BAC，AB=AC，连结BO、CO并延长交AC、AB于点E、F，则图中有（ ）对全等三角形。
A、1 B、2 C、3 D、4
9、若一次函数Y=kx+b的图象经过一、三、四象限，则应该满足
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
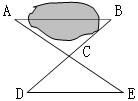10、如图，有一池塘，要测量池塘两端A、B的距离，可先在平地上取一个可以直接到达A和B的点C，连结AC并延长至E，使CE=AC，连结BC并延长至D，使CD=BC，连结DE，根据△ABC≌△EDC可知，量出DE的长，就是A、B的距离，这里△ABC≌△EDC的依据是（ ）
A.SAS B.ASA C.AAS D.SSS
二、填空题（每题3分，共30分）
11、已知：函数
,自变量x的取值范围是_________.
12、把直线Y=2X向下平移2个单位，得到的直线解析式为_____ ____ _ .
13、如图，已知：CD=BD，要得到△ADC≌△ADB，则还需要补充的条件是 _______ .
14、若一次函数y＝－x＋m²与y＝4x－1的图象交于x轴，则m的值为 ___
15、如图，若△ABC≌△ADE，∠EAC=35°,则∠BAE= ________
|
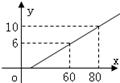16、某地长途汽车客运公司规定旅客可以随身携带一定重量的行李，如果 超过规定，则需购买行李票，行李票费用y（元）是行李重量x（千克）的一次函数，图象如图，则旅客最多可以免费携带 千克行李。
17、已知:一次函数y＝（k－1）x＋k的图象如图所示,则k的取值范围_______
18．某同学带10元钱去新华书店买数学辅导书，已知每册定价1元8角，设买书后余下的钱数y（元）和买书的册数x ，则y与x的函数解析式为____________.其中自变量x的取值范围 。
19、小明家上月的开支情况如图所示，其中教育上的支出是150元，则食物上的支出是 元。
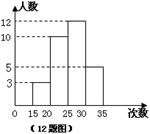
20、为了了解某校八年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图，请根据图示计算，仰卧起坐次数在25—30次的频率是 。
三、解答题
21、如图，平面直角坐标系中画出了函数y=kx+b的图象，
⑴ 根据图象，求k、b的值；（4分）
⑵ 在图中画出函数y=–4x+4的图象；（4分）
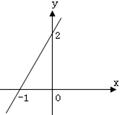⑶ 求x的取值范围，使函数y=kx+b的函数值大于函数y=–4x+4的函数值。（5分）
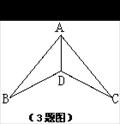
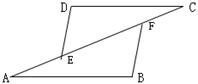22、如图，AB∥CD，AE=CF，AB=CD。 求证：DE=BF.
（8分）
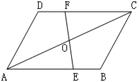23、如图，AB=CD，AD=BC，EB=DF,EF经过AC的中点O，分别交AB、CD于E、F。 求证：OE=OF.（10分）