八年级上学期第二次月考数学试卷
一、填空题（2、3题每题3分，其它每题2分，
共30分）
1. ABCD中，
，则
，
=
。
2. 菱形的两条对角线长分别是16cm和12cm，则菱形的边长是 ，高 ，面积是
。
3. 如图，正方形OABC的各顶点A、B、C的坐标如图，
则点A、B、C分别关于x轴，y轴，原点的坐标分别
是 ， ， 。
4.已知点A（
，
）在函数
的图像上，则
=
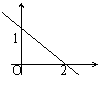5. 水池中原有水100立方米，现在以每分钟16立方米的速度向水池中注水，则水池中的总水量V（立方米）与注水时间t（分钟）之间的关系
。
6. 如图，一次函数图像如图所示，则函数关系式是 。
7．一次函数y=kx+b的图象经过P（1，0）和Q（0，1）两点，
则 P= Q=
8、请你写出一个经过点（1，1）的函数解析式 .
9、在函数
中，当自变量
满足 时，图象在第一象限.
10、已知函数y=(m-2)x-m2+4的图象经过原点则的值为 .
11、中国电信宣布，从2001年2月1日起，县城和农村电话收费标准一样，在县内通话3分钟内的收费是0.2元，每超1分钟加收0.1元，则电话费
（元）与通话时间
（
分，为正整数）的函数关系是
；
12、老师给出一个函数，甲、乙、丙各正确指出了这个函数的一个性质：
甲：函数的图象经过第一象限； 乙：函数的图象经过第三象限；
丙：在每个象限内，y随x的增大而减小．
请你根据他们的叙述构造满足上述性质的一个函数：
13.直线y=-2x+3与两条坐标轴所围成的面积为
14.若一次函数y1=kx-b图象经过第一、三、四象限，则一次函数y2=bx+k的图象经过第 象限。
二、选择题（每题3分，共30分）
1. 四边形ABCD中，AC、BD交于点O,则下列条件能判断四边形是正方形的有 。
① AC⊥BD,AO=CO=BO=DO ②AB=CD=AD=BC，AC=BD ③AO=BO=CO=DO
④
⑤AB∥CD，AB=BC=CD
A. 2个 B. 3个 C.4个 D.5个
2. 下面哪个点不在函数
的图像上（ ）
A.（-5，13） B.（0.5，2） C（3，0） D（1，1）
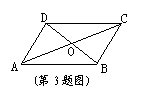3、如图，
ABCD中，对角线AC和BD相交于点O，如果AC=12、BD=10、AB=m，那么m的取什范围是( )
A．1＜m＜11 B．2＜m＜22
C．10＜m＜12 D．5＜m＜6
4．下列函数是一次函数的是（ ）
A．-
+y=0 B y=4x2-1 C y=
D 
5、四边形ABCD的对角线AC和BD相交于点O，设有下列条件：①AB=AD；②∠ DAB=900；③AO=CO，BO=DO；④矩形ABCD；⑤菱形ABCD，⑥正方形ABCD，则在下列推理不成立的是 ( )
A、①④
⑥ B、①③⑤ C、①②⑥ D、②③④
6. 在函数
中，y随x的增大而增大，则k的值可能是（ ）
A.1 B. 
C.2 D. 
7. 如图，右边坐标系中四边形的面积是（ ）
A. 4 B. 5.5 C. 4.5 D.5
8、点P（
）在直角坐标系的轴上，则点P的坐标为（ ）
A．(0，-2) B．(2，0) C．(4，0) D．(0，-4)
9、矩形ABCD中的顶点A、B、C、D按顺时针方向排列,若在平面直角坐标系内, B、D 两点对应的坐标分别是（2, 0）, (0, 0),且 A、C两点关于x轴对称.则C 点对应的坐标是（ ）
（A）（1, 1） (B)（1, －1）(C) （1, －2） (D) （, －）
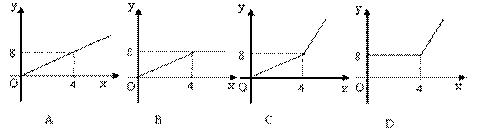
10、2004年6月3日中央新闻报道,为鼓励居民节约用水,北京市将出台新的居民用水收费标准:①若每月每户居民用水不超过4立方米,则按每立方米2元计算;②若每月每户居民用水超过4立方米,则超过部分按每立方米4.5元计算(不超过部分仍按每立方米2元计算).现假设该市某户居民某月用水立方米,水费为元,则与的函数关系用图象表示正确的是
三、解答题（共40分）
1、（本题7分）已知y与x+2成正比例，且x=1时y=-6
（1）求y与x之间的函数关系式；
（2）若点(a,2)在函数图象上，求a的值。
2、（本题6分）已知：如图，在△ABC中，AB=AC，E是AB中点，
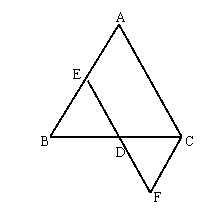以E为圆心，EB为半径画弧交BC于D点,
连接ED并延长到F，使DF=DE
求证：
|
如图，在方格直中建立直角坐标系，画出一次函数
y=4-2x的图像
4、（本题6分）图中折线ABC表示从甲地向乙地打长途电话时所需付的电话费y（元）与通话时间t（分钟）之间的关系图像。
① 从图像知，通话2分钟需付的电话费是 元。
② 当t≥3时求出该图像的解析式（写出求解过程）。
 |
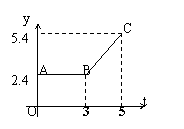③ 通话7分钟需付的电话费是多少元？
5、（本题8分）某公司到果园基地购买某种优质水果慰问医务工作者，果园基地对购买量在3000千克以上（含3000千克）的有两种销售方案。甲方案：每千克9元，由基地送货上门。乙方案：每千克8元，由顾客自己租车运回。已知该公司租车从基地到公司的运输费为5000元。
（1）分别写出该公司两种购买方案的付款y（元）与购买的水果量x（千克）之间的函数关系式，并写自变量x的取值范围。
甲方案：
乙方案：
（2）当购买量在什么范围时，选择哪种购买方案付款最少？并说明理由。
6、（本题8分）某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5米3的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1米3污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元：
(1)求出y与x的函数关系式.(纯利润=总收入-总支出)
(2)当y=106000时,求该厂在这个月中生产产品的件数.