八年级数学(上)期末检测题
班别: 姓名: 成绩:
一、选择题:(每小题3分,共15分)
1、下列运算不正确的是 ( )
A、 x2·x3=x5 B、 (x2)3=x6 C、 x3+x3=2x6 D、 (-2x)3=-8x3
2、下面有4个汽车标致图案,其中是轴对称图形的是 ( )

① ② ③ ④
A、②③④ B、①②③ C、①②④ D、①②④
3、如图,两条直线![]() 和
和![]() 和交点坐标可以看作下列方程组中( )的解.
和交点坐标可以看作下列方程组中( )的解.
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
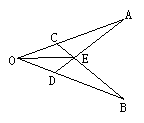
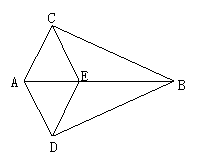
4、如图,已知OA=OB,OC=OD,AD,BC相交于E,则图中全等三角形的个数是( ).
A、5 B、4 C、3 D、2
 |
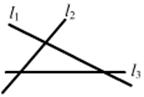
5、如图,l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有( )
A、四处 B、三处 C、二处 D、一处
二、填空题:(每题4分,共20分。请把正确答案填写在横线上)
6、因式分解:![]() ______________________.
______________________.
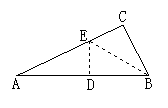
7、如图,AB=AC,要使![]() ,应添加的条件是____________.(添加一个即可)
,应添加的条件是____________.(添加一个即可)
 |
8、某校八年级(1)班有50名同学, 综合数值评价“运动与健康”方面的等级统计如图所示, 则该班“运动与健康”评价等级为A的人数是______________.

9、如图,把Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折痕ED,再沿BE折叠,C点恰好与D点重合,则∠A等于________度.
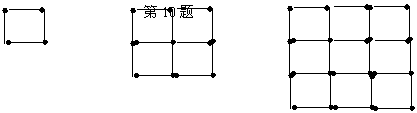 |
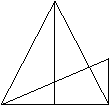
10、如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,当边长为n根火柴棍时,若摆出的正方形所用的火柴棍的根数为S,则S=______________(用含n的式子表示,n为正整数).
三、解下列各题:(每题6分,共30分)
11、(6分)已知一次函数![]() 的图象经过点A(-2,-3)及点B(1,6).
的图象经过点A(-2,-3)及点B(1,6).
(1).求此一次函数的解析式. (2).判断点C(![]() ,2)与点D(2,-5)是否在函数的图象上.
,2)与点D(2,-5)是否在函数的图象上.
 |
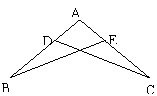
12、已知:如图,D是△ABC的边AB上一点,AB∥FC,DF交AC于点E,DE=EF。
求证:AE=CE。
13、计算:![]()
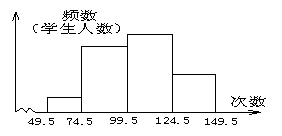
14、为了了解某校七年级男生的体能情况,从该校七年级抽取50名男生进行1分钟跳绳测试,把所得数据整理后,画出频数分布直方图(如图).已知图中从左到右第一、第二、第三、第四小组的频数的比为1:3:4:2.(1)求第二小组的频数和频率;(2)求所抽取的50名男生中,1分钟跳绳次数在100次以上(含100次)的人数占所抽取的男生人数的百分比.
15、已知:∠AOB,点M、N.
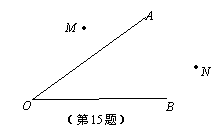 求作:点P,使点P在∠AOB的平分线上,且PM=PN.
求作:点P,使点P在∠AOB的平分线上,且PM=PN.
(要求:用尺规作图,保留作图痕迹,不写作法)
四、(每小题7分,共28分)
16、已知:如图,∠ACB=∠ADB=90°,AC=AD,E在AB上.
求证:CE=DE.
17、先化简,再求值:[(x+2y)(x-2y)-(x+4y)2]÷4y,其中x=-5,y=2.
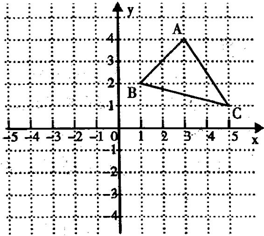
18、如图:
(1).写出A、B、C三点的坐标.
(2).若△ABC各顶点的横坐标不变,纵坐标都乘以-1,请你在同一坐标系中描出对应的点A′、B′、C′,并依次连接这三个点,所得的△A′B′C′与原△ABC有怎样的位置关系?
(3).在②的基础上,纵坐标都不变,横坐标都乘以-1,在同一坐标系中描出对应的点
A″、B″、C″,并依次连接这三个点,所得的△A″B″C″与原△ABC有怎样的位置关系?
19、阅读下列计算过程:
99×99+199=99![]() +2×99+1=(99+1)
+2×99+1=(99+1)![]() =100
=100![]() =10
=10![]()
(1).仿照上面的计算过程按步填空:
999×999+1999=____________=_______________=_____________=_____________;
9999×9999+19999=__________=_______________=______________=_______________。
(2).猜想×+等于多少?要求写出计算过程。
五、(每小题9分,共27分)
20、已知:如图,AB=AC,AD⊥BC于D,EC⊥BC,BE交AD于F,交AC于G且AD=BC=2CE.
 |
求证:(1).△ADC≌△BCE (2).BE⊥AC
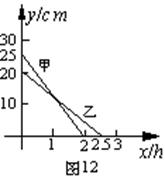 21、在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图12所示。请根据图象所提供的信息解答下列问题:
21、在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图12所示。请根据图象所提供的信息解答下列问题:
⑴.甲、乙两根蜡烛燃烧前的高度分别是___________________;
从点燃到燃尽所用的时间分别是___________________;
⑵.分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
⑶.当x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
22、已知:如图1,点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN交MC于点E,BM交CN于点F.
(1).求证:AN=BM; (2).求证:△CEF为等边三角形;
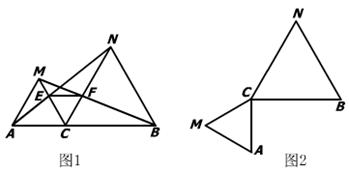 (3).将△ACM绕点C按逆时针方向旋转900,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明).
(3).将△ACM绕点C按逆时针方向旋转900,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立(不要求证明).
八年级数学(上)期末检测题
1、C 2、B 3、D 4、B 5、A 6、![]() 7、∠B=∠C或AD=AE或∠AEB=∠ADC等 8、19 9、30 10、S=2n(n+1)
7、∠B=∠C或AD=AE或∠AEB=∠ADC等 8、19 9、30 10、S=2n(n+1)
11、解:(1).设该一次函数的解析式为![]() ,依题意得:
,依题意得:
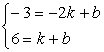 解得:
解得:![]() ∴该一次函数的解析式为
∴该一次函数的解析式为![]()
(2)当x=![]() 时,y=3×(
时,y=3×(![]() )+3=2; 当x=2时,y=3×2+3=9
)+3=2; 当x=2时,y=3×2+3=9
∴C(![]() ,2)在该函数的图象上,D(2,-5)不在该函数的图象上.
,2)在该函数的图象上,D(2,-5)不在该函数的图象上.
12、证明: ∵ AB∥FC ∴ ∠ADE=∠CFE; 在△AED和△CEF中:∠ADE=∠CFE、DE=FE、
∠AED=∠CEF ∴△AED≌△CEF(ASA) ∴AE=CE
13、解:原式![]()
![]()
14、解: 第二小组的频数=![]() ×50=15 第二小组的频率=15÷50=0.3 50×(
×50=15 第二小组的频率=15÷50=0.3 50×(![]() +
+![]() )÷50×100﹪=60﹪
)÷50×100﹪=60﹪
答: 1分钟跳绳次数在100次以上(含100次)的人数占所抽取的男生人数的60﹪
15、画出∠AOB的平分线 画出线段MN的垂直平分线 画出所求作的点P 写出结论.
16、证明:∵∠ACB=∠ADB=90° 在Rt△ABC和Rt△ABD中, AC=AD,AB=AB,
∴Rt△ABC≌Rt△ABD(HL) ∴∠ABC=∠ABD,BC=BD. 在△BEC和△BED中,
BC=BD,∠ABC=∠ABD,BE=BE, ∴△BEC≌△BED(SAS), ∴CE=DE.
17、解:原式![]()
![]()
![]()
![]()
当x=-5,y=2时,原式=-5×2-2×(-5)=-10+10=0
18.解:(1).A(3,4)、B(1,2)、C(5,1); (2).画图正确 △A′B′C′与△ABC关于x轴对称
(3). 画图正确 △A″B″C″与△ABC关于原点对称.
19、解:(1).999×999+1999=![]() =
=![]()
9999×9999+19999=![]()
(2).×+
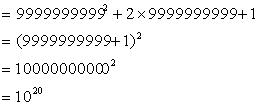
20、证明: (1)∵AB=AC,AD⊥BC ∴BD=DC=![]() ∵AD=BC=2CE ∴DC=CE
∵AD=BC=2CE ∴DC=CE
又∵AD⊥BC, EC⊥BC ∴∠ADC=∠BCE=90° 在△ADC和△BCE中DC=CE, ∠ADC=∠BCE, AD=BC
∴△ADC≌△BCE(SAS)
(2) ∵△ADC≌△BCE ∴∠DAC=∠CBE 又∵∠BFD=∠AFG ∴∠AGF=∠BDF=90° ∴BE⊥AC
21、解:⑴30cm,25cm;2h,2.5h;
⑵设甲蜡烛燃烧时y与x之间的函数关系式为![]() ,
,
由图可知,函数的图象过点(2,0),(0,30),
∴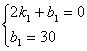 解得
解得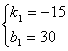 ∴
∴![]()
设乙蜡烛燃烧时y与x之间的函数关系式为![]() ,
,
由图可知,函数的图象过点(2.5,0),(0,25),
∴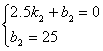 解得
解得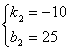 ∴
∴![]()
⑶由题意得![]() ,解得
,解得 ![]() ∴
当甲、乙两根蜡烛燃烧1h的时候高度相等。
∴
当甲、乙两根蜡烛燃烧1h的时候高度相等。
25、证明(1):∵△ACM, △CBN是等边三角形
∴AC=MC,BC=NC, ∠ACM=60°, ∠NCB=60°
在△CAN和△MCB中
AC=MC,∠ACN=∠MCB,NC= BC
∴△CAN≌△MCB(SAS)
∴AN=BM
(2): ∵△CAN≌△MCB
∴∠CAN=∠MCB
又∵∠MCF=180°-∠ACM-∠NCB=180°-60°-60°=60°
∴∠MCF=∠ACE
在△CAE和△CMF中
∠CAE=∠CMF,CA=CM,∠ACE=∠MCF
∴△CAE≌△CMF(ASA)
∴CE=CF
∴△CEF为等腰三角形,
又∵∠ECF=60°
∴△CEF为等边三角形.
(3)画图正确 ,结论仍然成立.