第十一章 一次函数检测题
班别： 姓名： 成绩：
一、选择题：（每小题3分，共30分）
1．下列函数中，自变量x的取值范围是x≥2的是（ ）
A．y=
B．y=
C．y=
D．y=
·
2．下面哪个点在函数y=
x+1的图象上（ ）
A．（2，1） B．（-2，1） C．（2，0） D．（-2，0）
3．下列函数中，y是x的正比例函数的是（ ）
A．y=2x-1 B．y=
C．y=2x2 D．y=-2x+1
4．一次函数y=-5x+3的图象经过的象限是（ ）
A．一、二、三 B．二、三、四 C．一、二、四 D．一、三、四
5．若函数y=（2m+1）x2+（1-2m）x（m为常数）是正比例函数，则m的值为（ ）
A．m>
B．m=
C．m<
D．m=-
6．若一次函数y=（3-k）x-k的图象经过第二、三、四象限，则k的取值范围是（ ）
A．k>3 B．0<k≤3 C．0≤k<3 D．0<k<3
7．已知一次函数的图象与直线y=-x+1平行，且过点（8，2），那么此一次函数的解析式为（ ）
A．y=-x-2 B．y=-x-6 C．y=-x+10 D．y=-x-1
8．汽车开始行驶时，油箱内有油40升，如果每小时耗油5升，则油箱内余油量y（升）与行驶时间t（时）的函数关系用图象表示应为下图中的（ ）
9．李老师骑自行车上班，最初以某一速度匀速行进，中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，如果准时到校．在课堂上，李老师请学生画出他行进的路程y（千米）与行进时间t（小时）的函数图象的示意图，同学们画出的图象如图所示，你认为正确的是（ ）
10．一次函数y=kx+b的图象经过点（2，-1）和（0，3），那么这个一次函数的解析式为（ ）
A．y=-2x+3 B．y=-3x+2
C．y=3x-2 D．y=x-3
二、填空题：（每小题3分，共30分）
11．已知自变量为x的函数y=mx+2-m是正比例函数，则m=________，该函数的解析式为_____．
12．若点（1，3）在正比例函数y=kx的图象上，则此函数的解析式为________．
13．已知一次函数y=kx+b的图象经过点A（1，3）和B（-1，-1），则此函数的解析式为_________．
14．若解方程x+2=3x-2得x=2，则当x_________时直线y=x+2上的点在直线y=3x-2上相应点的上方．
15．已知一次函数y=-x+a与y=x+b的图象相交于点（m，8），则a+b=_________．
16．若一次函数y=kx+b交于y轴的负半轴，且y的值随x的增大而减少，则k____0，b______0．（填“>”、“<”或“＝”）
17．已知直线y=x-3与y=2x+2的交点为（-5，-8），则方程组
的解是________．
18．已知一次函数y=-3x+1的图象经过点（a，1）和点（-2，b），则a=________，b=______．
19．如果直线y=-2x+k与两坐标轴所围成的三角形面积是9，则k的值为_____．
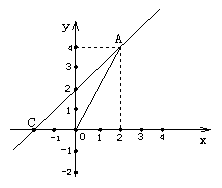20．如图，一次函数y=kx+b的图象经过A、B两点，与x轴交于点C，则此一次函数的解析式为__________，△AOC的面积为_________．
三、解答题：一定要细心哟！（共40分）
21．（6分）根据下列条件，确定函数关系式：
（1）y与x成正比，且当x=9时，y=16；
（2）y=kx+b的图象经过点（3，2）和点（-2，1）．
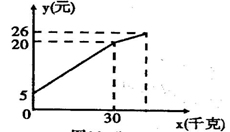
22．（6分）一次函数y=kx+b的图象如图所示：
（1）求出该一次函数的表达式
（2）当x=10时，y的值是多少？（3）当y=12时，x的值是多少？
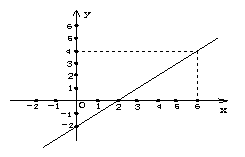
23．（8分）一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售．售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示，结合图象回答下列问题：
（1）农民自带的零钱是多少？ （2）降价前他每千克土豆出售的价格是多少？
（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？
24．（10分）已知雅美服装厂现有A种布料70米，B种布料52米，现计划用这两种布料生产M、N两种型号的时装共80套．已知做一套M型号的时装需用A种布料1.1米，B种布料0.4米，可获利50元；做一套N型号的时装需用A种布料0.6米，B种布料0.9米，可获利45元．设生产M型号的时装套数为x，用这批布料生产两种型号的时装所获得的总利润为y元．
①求y（元）与x（套）的函数关系式，并求出自变量的取值范围；
②当M型号的时装为多少套时，能使该厂所获利润最大？最大利润是多？
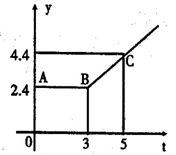
25．（10分）如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y（元）与通话时间t（分钟）之间的函数关系的图象．（1）写出y与t之间的函数关系式．（2）通话2分钟应付通话费多少元？通话7分钟呢？
第十一章 一次函数检测题答案
一、选择题：（每小题3分，共30分）
1．D 2．D 3．B 4．C 5．D 6．A 7．C 8．B 9．C 10．A
二、填空题：（每小题3分，共30分）
11．2；y=2x 12．y=3x 13．y=2x+1 14．<2 15．16
16．<；< 17．
18．0；7
19．±6
20．y=x+2；4
三、解答题：一定要细心哟！（共40分）
21. ①y=
x；②y=
x+
22. ①y=x-2；②y=8；③x=14 23. ①5元；②0.5元；③45千克
24．①y=50x+45（80-x）=5x+3600．
∵两种型号的时装共用A种布料[1.1x+0.6（80-x）]米，共用B种布料[0.4x+0.9（80-x）]米，∴ 解之得40≤x≤44，
而x为整数，
∴x=40，41，42，43，44，∴y与x的函数关系式是y=5x+3600（x=40，41，42，43，44）；
②∵y随x的增大而增大，∴当x=44时，y最大=3820，
即生产M型号的时装44套时，该厂所获利润最大，最大利润是3820元．
25. ①当0<t≤3时，y=2.4；当t>3时，y=t-0.6． ②2.4元；6.4元