11.3.3 一次函数与二元一次方程(组) 同步练习题
一、选择题
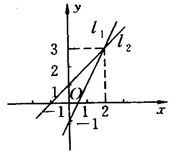
1．图中两直线L1，L2的交点坐标可以看作方程组( )的解．
A．
B. 
C．
D. 
2．把方程x+1=4y+
化为y=kx+b的形式，正确的是( )
A．y=
x+1 B．y=
x+
C．y=x+1 D．y=x+
3．若直线y=
+n与y=mx-1相交于点(1，-2)，则( )．
A．m=
，n=-
B．m=，n=-1； C．m=-1，n=- D．m=-3，n=-
4．直线y=x-6与直线y=-
x-
的交点坐标是( )．
A．(-8，-10) B．(0，-6)； C．(10，-1) D．以上答案均不对
5．在y=kx+b中，当x=1时y=2；当x=2时y=4，则k，b的值是( )．
A．
B. 
C．
D. 
6．直线kx-3y=8，2x+5y=-4交点的纵坐标为0，则k的值为( )
A．4 B．-4 C．2 D．-2
二、填空题
1．点(2，3)在一次函数y=2x-1的________；x=2，y=3是方程2x-y=1的_______．
2．已知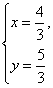
是方程组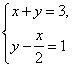
的解，那么一次函数y=3-x和y=+1的交点是________．
3．一次函数y=3x+7的图像与y轴的交点在二元一次方程-2x+by=18上，则b=_________．
4．已知关系x，y的二元一次方程3ax+2by=0和5ax-3by=19化成的两个一次函数的图像的交点坐标为(1，-1)，则a=_______，b=________．
5．已知一次函数y=-x+m和y=x+n的图像都经过A(-2，0)，则A点可看成方程组________的解．
6．已知方程组
的解为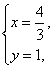
则一次函数y=3x-3与y=-x+3的交点P的坐标是______．
三、解答题
1．若直线y=ax+7经过一次函数y=4-3x和y=2x-1的交点，求a的值．
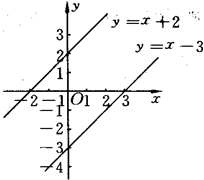
2．(1)在同一直角坐标系中作出一次函数y=x+2，y=x-3的图像．
(2)两者的图像有何关系?
(3)你能找出一组数适合方程x-y=2，x-y=3吗?_________________，这说明方程组
________．
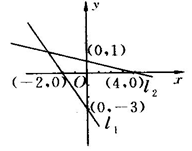
3．如图所示，求两直线的解析式及图像的交点坐标．
探究应用拓展性训练
1．(学科内综合题)在直角坐标系中，直线L1经过点(2，3)和(-1，-3)，直线L2经过原点，且与直线L1交于点(-2，a)．
(1)求a的值．
(2)(-2，a)可看成怎样的二元一次方程组的解?
(3)设交点为P，直线L1与y轴交于点A，你能求出△APO的面积吗?
2．(探究题)已知两条直线a1x+b1y=c1和a2x+b2y=c2，当
≠
时，方程组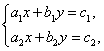
有唯一解?这两条直线相交?你知道当a1，a2，b1，b2，c1，c2分别满足什么条件时，方程组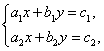无解?无数多组解?这时对应的两条直线的位置关系是怎样的?
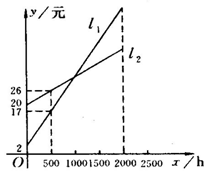
3．(2004年福州卷)如图，L1，L2分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费，单位：元)与照明时间x(h)的函数图像，假设两种灯的使用寿命都是2000h，照明效果一样．
(1)根据图像分别求出L1，L2的函数关系式．
(2)当照明时间为多少时，两种灯的费用相等?
(3)小亮房间计划照明2500h，他买了一个白炽灯和一个节能灯，请你帮他设计最省钱的用灯方法(直接给出答案，不必写出解答过程)．
11.3.3 一次函数与二元一次方程(组) 同步练习答案：
一、选择题
1．B 解析：设L1的关系式为y=kx-1，将x=2，y=3代入，得3=2k-1，解得k=2．
∴L1的关系式为y=2x-1，即2x-y=1．
设L2的关系式为y=kx+1，将x=2，y=3代入，得3=2k+1，解得k=1．
∴L2的关系式为y=x+1，即x-y=-1．
故应选B．
2．B 解析：∵x+1=4y+，∴4y=x+1-，4y=
x+1，y=x+．故应选B．
3．C 解析：把x=1，y=-2代入y=+n得-2=+n，n=-2-，n=-.
把x=1，y=-2代入y=mx-1得-2=m-1，m=-2+1，m=-1，故应选C．
4．C 解析：解方程组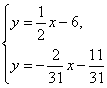
，得
∴直线y=x-6与直线y=-x-
的交点为(10，-1)，故应选C．
5．B 解析：把
分别代入y=kx+b，得
解得
故应选B．
6．B 解析：把y=0代入2x+5y=-4，得2x=-4，x=-2．
所以交点坐标为(-2，0)．
把x=-2，y=0代入kx-3y=8，得-2k=8，k=-4，故应选B．
二、填空题
1．解析：当x=2时，y=2x-1=2×2-1=3，∴(2，3)在一次函数y=2x-1的图像上．
即x=2，y=3是方程2x-y=1的解．
答案：图像上 解
2．解析：因为方程组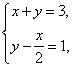
中的两个方程变形后为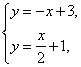
所以函数y=3-x与y=+1的交点坐标就是二元一次方程组的解，即为（
，
）。
答案：（，）
提示：此题不用解方程组，根据一次函数与二元一次方程组的关系，结合已知就可得到答案．
3．解析：y=3x+7与y轴的交点的坐标为(0，7)．
把x=0，y=7代入-2x+by=18，得7b=18，b=
。
答案：
4．解析：把x=1，y=-1分别代入3ax+2by=0，5ax-3by=19得
解得
答案：2 3
5．解析：把
代入y=-x+m，得0=3+m，∴m=-3，
∴y=-x-3，即x+y=-3．
把 代入y=x+n，得0=-1+n，
∴n=1，∴y=x+1，即x-y=-1．
∴A(-2，0)可看作方程组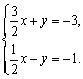
的解．
答案：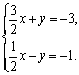
6．解析：方程组
中的两个方程分别变形即为y=3x-3与y=-x+3，
故两函数的交点坐标为方程组的解，即（，1）。
答案：（，1）
三、解答题
1．解析：解方程组
得
∴两函数的交点坐标为(1，1)．
把x=1，y=1代入y=ax+7，得1=a+7，解得a=-6．
2．解析：(1)图像如答图所示．
(2)y=x+2与y=x-3的图像平行．
(3)y=x+2即x-y=-2，y=x-3即x-y=3．
∵直线y=x+2与y=x-3无交点，
∴方程组
无解．
提示：当两直线平行时无交点，即由两个函数解析式组成的二元一次方程组无解．
3．解析：设L1的解析式为y=k1x+b1，
把
分别代入，
得
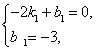解得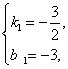
∴L1的解析式为y=-x-3．
设L2的解析式为y=k2x+b2，把
分别代入，
得
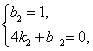解得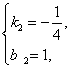
∴L的解析式为y=-x+1．
解方程组
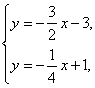得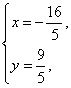
∴L1与L2的交点坐标为（-
，
）。
探究应用拓展性训练答案：
1．(1)设L的关系式为y=kx+b，把(2，3)，(-1，-3)分别代入，
得
解得
∴L1的解析式为y=2x-1．
当x=-2时，y=-4-1=5，即a=-5．
(2)设L2的关系式为y=kx，把(2，-5)代入得-5=2k，k=-,
∴L1的关系式为y=-x．
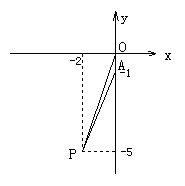∴(-2，a)是方程组
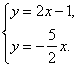的解．
(3)如答图，把x=0代入y=2x-1，得y=-1．
∴点A的坐标为A(0，-1)．
又∵P(-2，-5)，
∴S△APO=·OA·2=×│-1│×2=×1×2=1．
2．解析：对于两个一次函数y1=k1x+b1，y2=k2x+b2而言：
(1)当k1≠k2时，两直线相交．
(2)当k1=k2，且b1≠b2时，两直线平行．
(3)当k1=k2，且b1=b2时，两直线重合．
故对两直线a1x+b1y=c1与a2x+b2y=c2来说：
(1)当 ≠时，两直线相交，即方程组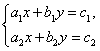
有唯一解．
(2)当 =≠
时，方程组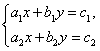无解，两直线平行．
(3)当==时，方程组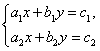有无数多个解，两直线重合．
提示：方程组的解就是两个一次函数的交点坐标，当两直线只有一个公共点时，方程组有唯一解；当两直线平行(无公共点)时，方程组无解；当两直线有无数个公共点时，方程组有无数多个解．
3．解析：(1)设L1的解析式为y1=k1x+2，由图像得17=500k1+2，解得k=0．03，
∴y1=0．03x+2(0≤x≤2000)．
设L2的解析式为y2=k2x+20，
由图像得26=500k2+20，解得k2=0．012．
∴y2=0．012x+20(0≤x≤2000)．
(2)当y1=y2时，两种灯的费用相等，
∴0．03x+2=0．012x+20，解得x=1000．
∴当照明时间为1000h时，两种灯的费用相等．
(3)最省钱的用灯方法：
节能灯使用2000h，白炽灯使用500h．
提示：本题的第(2)题，只要求出L1与L2交点的横坐标即可．第(1)题中，求出L1与L2的解析式，一定不能忽略自变量x的取值范围，这为第(3)题的分析、设计方案作了铺垫．在第(3)题中，当x>1000h时，L2在L1的下方，即采用节能灯省钱，因x最多为2000h，故求以下的500h应采用白炽灯．