与二次根式有关的规律探究
1、我们知道形如
的数可以化简，其化简的目的主要先把原数分母中的无理数化为有理数，如： 
，
这样的化简过程叫做分母有理化。我们把
叫做的有理化因式，
叫
做的有理化因式，完成下列各题。
（1）
的有理化因式是
，
的有理化因式是 ，
（2）化简：
2、综合探究：
（1）
比较大小：
，
解：（填空完成解答过程，填“>、=、<”）
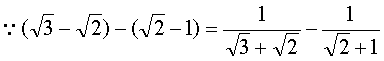
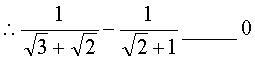
同理有：
（2） 由（1）中比较的结果，猜想：
对（2）中的猜想加以证明。
3、观察以下各式：
利用以上规律计算：
 |
4、观察下列各式及验证过程：
式①：
验证：
式②：
验证：
⑴ 针对上述式①、式②的规律，请再写出一条按以上规律变化的式子；
⑵ 请写出满足上述规律的用n（n为任意自然数，且n≥2）表示的等式。
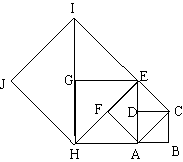5、如图，如果以正方形ABCD的对角线
AC为边作第二个正方形ACEF，
再以对角线AE为边作第三个正方形
AEGH，如此下去，…，已知正方形
ABCD的边长a1为1，按上述方法所作
的正方形的边长依次为a1， a2…，an
（n为正整数），那么第8个正方形的
边长a8＝_______。
6、先阅读下列的解答过程，然后再解答：
形如
的化简，只要我们找到两个数a、b，使
，
，使得
，
，那么便有：
例如：化简
解：首先把化为
，这里
，
，由于4+3=7，
即
，
∴==
由上述例题的方法化简：
；