第17章《反比例函数》单元测试题
一、选择题：(每题3分，共27分)
1、下列函数中，不属于y是x的反比例函数的是（ ）
A、
B、
C、
D、
2、有以下判断：①圆面积公式
中，面积S与半径r成正比例；②运动的时间与速度成反比例；③当电压不变时，电流强度和电阻成反比例；④圆柱体的体积公式
中，当体积V不变时，圆柱的高h与底面半径r的平方成反比例，其中错误的有（ ）
A、1个 B、2个 C、3个 D、4个
3、若y与x成反比例，x与z成正比例，则y是z的（ ）
A、 正比例函数 B、 反比例函数 C、 一次函数 D、 不能确定
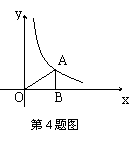4、如图，A为反比例函数
图象上一点，AB垂直x轴于B点，若S△AOB＝3，则k的值为（ ）
A、6 B、3 C、+3或-3 D、+6或-6
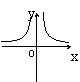
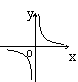
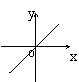
5、如果矩形的面积为6cm2，那么它的长
cm与宽
cm之间的函数关系用图象表示大致（ ）
 |  | ||||||
 | |||||||
 | |||||||
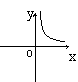A B C D
6、在同一直角坐标平面内，如果直线
与双曲线
没有交点，那么
和
的关系一定是（ ）
A 、<0， >0 B
、>0， <0 C 、、同号 D 、、异号
7、下列函数中y随x的增大而减小的是（ ）
A、
B、
C、
D、
8、已知
是反比例函数
的图象上三点，且
，则
的大小关系是（ ）
A、
B、
C、
D、
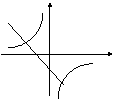
9、在同一坐标系中，函数和
的图象大致是 （ ）
 | |||||||
 |  |  | |||||
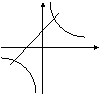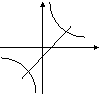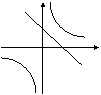A B C D
二、填空题：(每题4分，共36分)
11、已知反比例函数
的图象经过点（3，4），则
=
；
12、若反比例函数
的图象经过二、四象限，则k= _______.
13、已知是的反比例函数，当=3时，=4，则当=2时=_________。
14、已知A（-3，
）和B（m+3,2）都是反比例函数的图像上的两点，则m=______.
15、对于函数
，当
时，y的取值范围是______
______；当
时且
时，y的取值范围是y
______1，或y ______。（提示：利用图像解答）
16、将
代入反比例函数
中,所得函数记为y1,又将x=y1+1代入函数中,所得函数记为y2,再持x=y2+1代入函数中,所得函数记为y3,如此继续下去,则y2005=_________;
17、、已知y-2与x成反比例，当x=3时，y=1，则y与x之间的函数关系式 。
18.设有反比例函数
，（
）、
为其图象上两点，若
，则k 的取值范围是
。
19、一反比例函数与y=x无交点，且反比例函数图像上的任意一点到两坐标轴距离乘积等于5，则反比例函数的解析式为 。
三、画图题（5分）
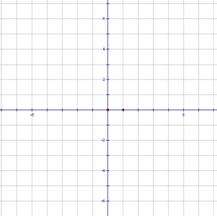20、在下面的平面直角坐标系中画出函数
的图像。
21．（12分）已知一次函数
的图象与反比例函数
的图象交于A，B两点，且A点的横坐标与B点的纵坐标都是
；
(1)一次函数的解析式
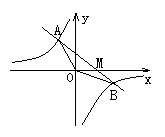(2)△AOB的面积。
（3）x取何值反比例函数的值大于一次函数的值。
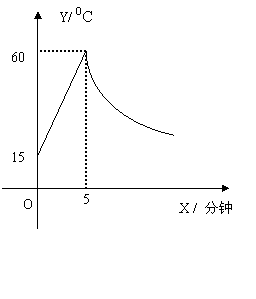
22、（8分）制作一种产品，需先将材料加热到60 0C后，再进行操作，设刻材料温度为y 0C，从开始加热计算的时间为x分钟，据了解，该材料加热后，温度y与时间成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系(如图)，已知该材料在操作加工前的温度为15 0C，加热5分钟后温度达到60 0C。
(1) 分别求出将材料加热和停止加热进行操作是，y与x的函数关系；
(2) 拫据工艺要求，当材料的温度低于15 0C时，须停止操作，那么从开始加热到停止操作，共经历了多长时间？
 |
23、（12分）某气球内充满了一定质量的气球,当温度不变时,气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数,其图象如图所示(千帕是一种压强单位)
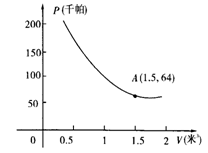（1）写出这个函数的解析式；
（2）当气球的体积为0.8立方米时,气球内的气压是多少千帕？
（3）当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米？
答案：
选择题：１、Ｂ 2、Ｂ 3、Ｂ 4、Ａ 5、Ｃ 6、Ｄ 7、 Ｃ
8、Ｂ 9、Ａ
填空题：10、12 11、-3 12、6 13、-6 14、-1。5 15、0 1 ≥＜0 16、 
17、k<-1
18、
三、画图题19、（略）
解答题20、（1） y=-x+2 （2）6 （3）-2<x<0 x>4时
21、y=9x+15(0≤x≤5) 
(x≥5) 20分钟
22、
（x>0） 120 2/3