等腰三角形
练习题
(第一课时)
一、选择题
1．等腰三角形的对称轴是（ ）
A．顶角的平分线 B．底边上的高
C．底边上的中线 D．底边上的高所在的直线
2．等腰三角形有两条边长为4cm和9cm，则该三角形的周长是（ ）
A．17cm B．22cm C．17cm或22cm D．18cm
3．等腰三角形的顶角是80°，则一腰上的高与底边的夹角是（ ）
A．40° B．50° C．60° D．30°
4．等腰三角形的一个外角是80°，则其底角是（ ）
A．100° B．100°或40° C．40° D．80°
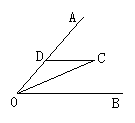
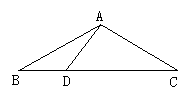
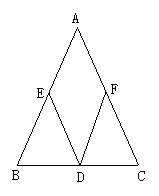5．如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（ ）
A．80° B．90° C．100° D．108°
二、填空题
6．等腰△ABC的底角是60°，则顶角是________度．
7．等腰三角形“三线合一”是指___________．
8．等腰三角形的顶角是n°，则两个底角的角平分线所夹的钝角是_________．
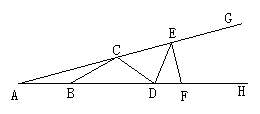
9．如图，△ABC中AB=AC，EB=BD=DC=CF，∠A=40°，则∠EDF的度数是_____．
10．△ABC中，AB=AC．点D在BC边上
（1）∵AD平分∠BAC，∴_______=________；________⊥_________；
（2）∵AD是中线，∴∠________=∠________；________⊥________；
（3）∵AD⊥BC，∴∠________=∠_______；_______=_______．
三、解答题
11．已知△ABC中AB=AC，AD⊥BC于D，若△ABC、△ABD的周长分别是20cm和16cm，求AD的长．
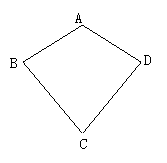
12．如图，在四边形ABCD中，AB=AD，CB=CD，求证：∠ABC=∠ADC.
13．已知△ABC中AB=AC，点P是底边的中点，PD⊥AB，PE⊥AC，垂足分别是D、E，
求证：PD=PE.
四、探究题
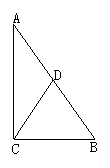
14．如图，CD是△ABC的中线，且CD= 
AB，你知道∠ACB的度数是多少吗？由此你能得到一个什么结论？请叙述出来与你的同伴交流．
答案:
1．D 2．B 3．A 4．C 5．B 6．60
7．等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合
8．（90+ n）° 9．70° 10．略 11．6cm
12．连接BD，∵AB=AD，∴∠ABD=∠ADB．∵CB=CD，∴∠CBD=∠CDB．∴∠ABC=∠ADC
13．连接AP，证明AP平分∠BAC．
14．∠ACB=90°．结论：若一个三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形
练习题
(第二课时)
一、选择题
1．如图1，已知OC平分∠AOB，CD∥OB，若OD=3cm，则CD等于（ ）
A．3cm B．4cm C．1.5cm D．2cm
（1） (2) (3)
2．△ABC中AB=AC，∠A=36°，BD平分∠ABC交AC于D，则图中的等腰三角形有（ ）
A．1个 B．2个 C．3个 D．4个
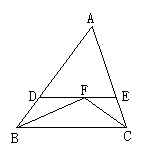
3．如图2，△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论：①△BDF和△CEF都是等腰三角形；②DE=BD+CE；③△ADE的周长等于AB与AC的和；④BF=CF．其中正确的有（ ）
A．①②③ B．①②③④ C．①② D．①
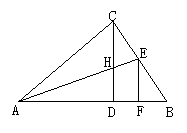
4．如图3，Rt△ABC中，CD是斜边AB上的高，角平分线AE交CD于H，EF⊥AB于F，则下列结论中不正确的是（ ）
A．∠ACD=∠B B．CH=CE=EF C．CH=HD D．AC=AF
二、填空题
5．△ABC中，∠A=65°，∠B=50°，则AB：BC=_________．
6．已知AD是△ABC的外角∠EAC的平分线，要使AD∥BC，则△ABC的边一定满足________．
7．△ABC中，∠C=∠B，D、E分别是AB、AC上的点，AE=2cm，且DE∥BC，则AD=________．
8．一灯塔P在小岛A的北偏西25°，从小岛A沿正北方向前进30海里后到达小岛，此时测得灯塔P在北偏西50°方向，则P与小岛B相距________．
三、解答题
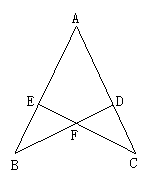
9．如图，已知AB=AC，E、D分别在AB、AC上，BD与CE交于点F，且∠ABD=∠ACE，
求证：BF=CF．
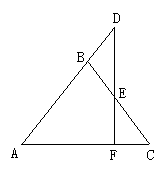
10．如图，△ABC中BA=BC，点D是AB延长线上一点，DF⊥AC于F交BC于E，
求证：△DBE是等腰三角形．
四、探究题
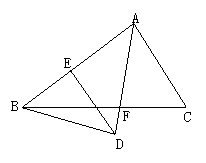
11．如图，AF是△ABC的角平分线，BD⊥AF交AF的延长线于D，DE∥AC交AB于E，
求证：AE=BE．
答案:
1．A 2．C 3．A 4．C 5．1 6．AB=AC 7．2cm 8．30海里
9．连接BC，∵AB=AC，∴∠ABC=∠ACB，又∵∠ABD=∠ACE，∴∠FBC=∠FCB，∴FB=FC
10．证明∠D=∠BED
11．证明∠EAD=∠EDA，∠EBD=∠EDB分别得到AE=DE，BE=DE
等边三角形
练习题
一、选择题
1．正△ABC的两条角平分线BD和CE交于点I，则∠BIC等于（ ）
A．60° B．90° C．120° D．150°
2．下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（ ）
A．①②③ B．①②④ C．①③ D．①②③④
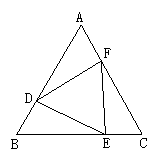
3．如图，D、E、F分别是等边△ABC各边上的点，且AD=BE=CF，则△DEF的形状是（ ）
A．等边三角形 B．腰和底边不相等的等腰三角形
C．直角三角形 D．不等边三角形
4．Rt△ABC中，CD是斜边AB上的高，∠B=30°，AD=2cm，则AB的长度是（ ）
A．2cm B．4cm C．8cm D．16cm
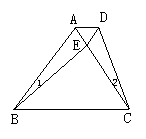
5．如图，E是等边△ABC中AC边上的点，∠1=∠2，BE=CD，则对△ADE的形状最准备的判断是（ ）
A．等腰三角形 B．等边三角形 C．不等边三角形 D．不能确定形状
二、填空题
6．△ABC中，AB=AC，∠A=∠C，则∠B=_______．
7．已知AD是等边△ABC的高，BE是AC边的中线，AD与BE交于点F，则∠AFE=______．
8．等边三角形是轴对称图形，它有______条对称轴，分别是_____________．
9．△ABC中，∠B=∠C=15°，AB=2cm，CD⊥AB交BA的延长线于点D，则CD的长度是_______．
三、解答题
10．已知D、E分别是等边△ABC中AB、AC上的点，且AE=BD，求BE与CD的夹角是多少度？
11．如图，△ABC中，AB=AC，∠BAC=120°，AD⊥AC交BC于点D，求证：BC=3AD.
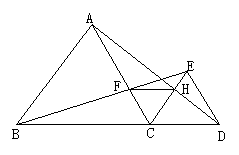
12．如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H，①求证：△BCE≌△ACD；②求证：CF=CH；③判断△CFH的形状并说明理由．
四、探究题
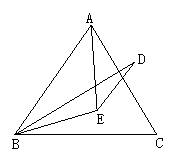
13．如图，点E是等边△ABC内一点，且EA=EB，△ABC外一点D满足BD=AC，且BE平分∠DBC，求∠BDE的度数．（提示：连接CE）
答案：
1．C 2．D 3．A 4．C 5．B 6．60° 7．60°
8．三；三边的垂直平分线 9．1cm 10．60°或120°
11．∵AB=AC，∠BAC=120°，∴∠B=∠C=30°，
∴在Rt△ADC中CD=2AD，
∵∠BAC=120°，∴∠BAD=120°-90°=30°，
∴∠B=∠BAD，∴AD=BD，∴BC=3AD
12．①∵∠ACB=∠DCE=60°，∴∠BCE=∠ACD．
又∵BC=AC，CE=CD，∴△BCE≌△ACD；
②证明△BCF≌△ACH；
③△CFH是等边三角形．
13．连接CE，先证明△BCE≌△ACE得到∠BCE=∠ACE=30°，
再证明△BDE≌△BCE得到∠BDE=∠BCE=30°