八年级数学上学期期中考试
数 学 试 题
（ 时间：90分钟 满分：100分）
姓名 分数
一、选择题（每小题3分，共30分）
1、下列各数中无理数的个数有（ ）
－0.333… ，
，
，－
，3. ，－
，
，
－１，
2.010101…（相邻两个1之间有1个0）， （
＋１）0
A、3个 B、4个 C、5个 D、6个
2、下列条件中，不能判定四边形ABCD是平行四边形的条件是（ ）
A、AB平行且等于CD B、∠A=∠C, ∠B=∠D
C、AB∥CD , AD=BC C、AB=CD , AD=BC
3、下列各式中正确的是（ ）
A、
B、
C、
D、
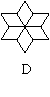
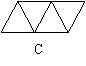
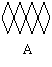4、下列四个图形中，不能通过基本图形平移得到的是（ ）
 | |||
 | |||
5、大于
且不大于
的整数有（ ）
A、9个 B、8个 C、7个 D、6个
6、对角线互相垂直且相等的四边形一定是（ ）
A、正方形 B、矩形 C、菱形 D、以上都不是
7、下列四组数中，不是勾股数的一组是（ ）
A、3，4，5 B、1.5，2，2.5 C、5，12，13 D、9，40，41
8、一个数的立方根与它的平方根完全相同，则这个数是（ ）
A、1 B、-1 C、1或-1 D、0
9、已知菱形的周长为40，一条对角线长为12，则这个菱形的面积为（ ）
A、190 B、96 C、48 D、40
10、如图，在 ABCD 中，AE⊥BC于E, AF⊥CD于F,若AE=4,AF=6, ABCD的周长为40，则 ABCD的面积为（
）
A、24 B、36 C、40 D、48
二、填空题（每小题3分，共24分）
11、
的算术平方根是 ；
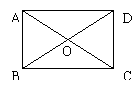
12、如右图，矩形ABCD的对角线交于点O , ∠AOD=120°,
AB=4cm , 那么矩形的对角线长为 ，
BC= ；
13、在平行四边形ABCD中，∠A+∠C=140°,那么∠A= , ∠B= ;
14、如果
有意义，则x的取值范围是
；
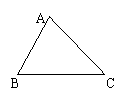
15、在Rt△ABC中,∠C=900,
若a=9,b=12,则c=_____;
若a=7,c=25,则b=_______;
若a:b=3:4,c=10,则SRt△ABC=______.
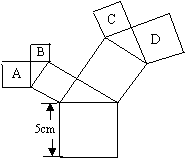
16、如图所有的四边形都是正方形,所有的三角
形都是直角三角形,其中最大的正方形的边
长为5 cm,则正方形A,B,C,D的面积之和为______cm2.
17、在Rt△ABC中,∠C=900,AC=5,BC=12，则斜边AB边上的高CD为_________.
18、直角三角形有两边长分别为3和4,则另一条边长为 __________.
三、解答题（共46分）
19、计算题（每小题4分，共12分）：
1
2
3
20、操作题（每小题6分，共12分）
1如图，正方形网格中每个小正方形的边长都是1，任
意连接这些小正方形的顶点，可得到一些线段。请你在
图中画出线段AB,CD,EF,
且使AB=
, CD=, EF=
。
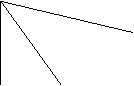
2将△ABC平移后，点A移到点A’的位置，请先作出平移后的△A’B’C’，再将平移后的三角形绕点C’顺时针旋转90°
 |
. A’
21、小民想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.（5分）
解:
22、如图是美国总统Garfield于1876年给出的一种验证勾股定理的办法，你能利用它验证勾股定理吗？ （5分）
证明：
 |
b
c c
a
a b
22、如图，在矩形ABCD中，AC与BD交于点O,过点A、C分别作AF∥DB,CE∥DB,AF交CB的延长线于F,CE交AB的延长线于E.试判断四边形AFEC是什么四边形？并说明理由。（6分）
 |
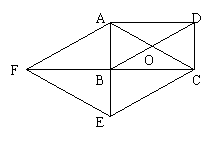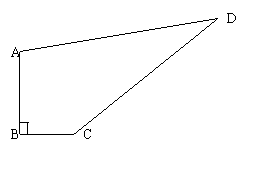23、有一块如图所示的四边形的实验田，为了确定这块四边形试验田的面积，测得AB=4m, BC=3m, CD=12m, AD=13m，且∠ABC=90°。请你利用以上数据结合所学知识计算出这块试验田的面积。（6分）
附加题：
先观察下列各式：
（1）
（2）
（3）
（4）
猜想：
的变形结果并进行验证；
用字母n表示上述的规律并进行验证（n为任意的自然数，且n≥2）
解: