八年级数学特殊的平行四边形测试题
考试时间：100分钟，满分：120分
一、填空题（每题3分，共30分）
1．用一把刻度尺来判定一个零件是矩形的方法是 。
2．如果边长分别为4cm和5cm的矩形与一个正方形的面积相等，那么这个正方形的边长为______cm．
3．已知菱形两条对角线的长分别为5cm和8cm，则这个菱形的面积是 cm2．
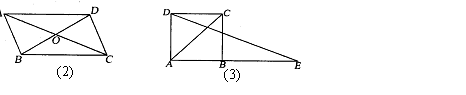
4．如图1，DE∥BC，DF∥AC，EF∥AB，图中共有_______个平行四边形．
5若四边形ABCD是平行四边形，请补充条件
(写一个即可)，使四边形ABCD是菱形．
6．如图2，在平行四边形ABCD中，已知对角线AC和BD相交于点O，△ABO的周长为17，AB＝6，那么对角线AC＋BD＝
⒎以正方形ABCD的边BC 为边做等边△BCE，则∠AED的度数为 。
8．如图3，延长正方形ABCD的边AB到E，使BE＝AC，则∠E＝ °
9．已知菱形ABCD的边长为6，∠A＝60°，如果点P是菱形内一点，且PB＝PD＝2
那么AP的长为 ．
10．在平面直角坐标系中，点A、B、C的坐标分别是A(－2，5)，
B(－3，－1)，C(1，－1)，在第一象限内找一点D，使四边形
ABCD是平行四边形，那么点D的坐标是 ．
二、选择题（每题3分，共30分）
11．如图4在平行四边形ABCD中，∠B=110°，延长AD至F，延长CD至E，连结EF，则∠E＋∠F＝( )
A．110° B．30° C．50° D．70°
12．菱形具有而矩形不具有的性质是 ( )
A．对角相等 B．四边相等
C．对角线互相平分 D．四角相等
13．如图5，平行四边形ABCD中，对角线AC、BD交于点O，
点E是BC的中点．若OE=3 cm，则AB的长为 ( )
A．3 cm B．6 cm C．9 cm D．12 cm
14．已知：如图6，在矩形ABCD中，E、F、G、H分别为边
AB、BC、CD、DA的中点．若AB＝2，AD＝4，
则图中阴影部分的面积为 ( )
A．8 B．6 C．4 D．3
15．将两块能完全重合的两张等腰直角三角形纸片拼成下列图形：①平行四边形（不包括菱形、矩形、正方形）②矩形③正方形④等边三角形⑤等腰直角三角形 ( )
A．①③⑤ B．②③⑤ C．①②③ D．①③④⑤
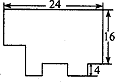
16．如图7是一块电脑主板的示意图，每一转角处都是
直角，数据如图所示(单位：mm)，则该主板的周长
是 ( )
A．88 mm B．96 mm C．80 mm D．84 mm
17、下列汽车标志中，是中心对称图形但不是轴对称图形的有（ ）个。
 |
（A）2 （B）3 （C）4 （D）5
 |
18、小明将下列 4张牌中的3张旋转180°后得到，
 |
没有动的牌是（ ）。
（A）2
（B）4
（C）6
（D）
8
19、四边形ABCD，仅从下列条件中任取两个加以组合，使得ABCD是平行四边形，一共有多少种不同的组合？（ ）
AB∥CD BC∥AD AB=CD BC=AD
（A）2组 （B）3组 （C）4组 （D）6组
20、下列说法错误的是（ ）
（A）一组对边平行且一组对角相等的四边形是平行四边形。
（B） 每组邻边都相等的四边形是菱形。
（C） 对角线互相垂直的平行四边形是正方形。
（D）四个角都相等的四边形是矩形。
三、阅读理解题（每空2分，共8分）
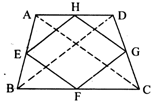
21、如图8，在四边形ABCD中，E、F、G、H分
别是AB、BC、CD、DA边上的中点，阅读下列材料，
⑴连结AC、BD，由三角形中位线的性质定理可证四边形 EFGH是 。
⑵对角线AC、BD满足条件 时，四边形 EFGH是矩形。
⑶对角线AC、BD满足条件 时，四边形 EFGH是菱形。
⑷对角线AC、BD满足条件 时，四边形 EFGH是正方形。
四、解答题（每题8分，共16分）
22、如图9，四边形ABCD是菱形，对角线AC＝8 cm ,
BD＝6 cm,
DH⊥AB于H，求：DH的长
23、已知：如图10，菱形ABCD的周长为16 cm，
∠ABC＝60°，对角线AC和BD相交于点O，
求AC和BD的长。
五、证明题（8分＋8分＋10分＋10分）
24、如图11，在正方形ABCD中，P为对角线BD上一点，
PE⊥BC，垂足为E， PF⊥CD，垂足为F，
求证：EF＝AP
25、在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
⑴试说明:DE=DF
⑵只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明
26、如图， ABCD中，AE平分∠BAD交BC于E，EF∥AB交AD于F，
试问：四边形ABEF是什么图形吗？
请说明理由。
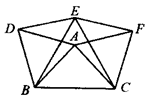
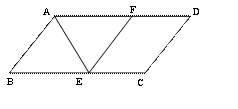
27、如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形，即△ABD、
△BCE、△ACF，请回答下列问题：
（1）四边形ADEF是什么四边形？并说明理由
（2）当△ABC满足什么条件时，四边形ADEF是菱形？
（3）当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在．
 | |||
 | |||
参考答案
一、填空题⒈先测量两组对边是否相等，然后测量两条对角线是否相等。⒉2
3.20 4、3 5、AC⊥BD 6、22 7、150°或15° 8、22.5° 9、4 10、（2 ，5）
二 、选择题
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| D | B | B | C | A | B | A | C | C | C |
三、阅读填空21、⑴平行四边形 ⑵ AC⊥BD ⑶ AC＝BD ⑷ AC⊥BD且 AC＝BD
四、解答题 22、4.8 cm 23、AC＝4 cm , BD＝4
24 证明：连结PC∵四边形ABCD为平行四边形 AB＝AC ，∠ABD＝∠DPC ∠BCD＝90°∵BP＝BP∴△ABP≌△CBP∴AP = CP∵PE⊥BC，PF⊥DC∴四边形PECF为矩形∴EF＝PC∴EF＝AP
25、证明：⑴连结AD∵AB＝AC，D为BC的中点∴AD为∠BAC的平分线∵DE⊥AB ， DF⊥AC∴DE＝DF
⑵∠BAC＝90° DE⊥DF
26、菱形
∵四边形ABCD为平行四边形∴AD∥BC ，∠2＝∠3
∵AB∥EF∴四边形ABED为平行四边形
∵∠2＝∠1∴∠1＝∠3∴AB＝BE∴四边形ABED为菱形
27、⑴平行四边形
⑵当AB＝AC即△ABC为等腰三角形时，四边形ADEF为菱形
⑶△ABC为等边三角形时，四边形ADEF不存在