八年级数学下学期第十章测试卷（苏教版）
个人档案：班级 姓名 学号
一、 小试身手（这里共有20个宝物，你只要找到12个就可进入下一关。每题藏有两个宝物）
1．在比例尺为1：100 000的地图上，量得两地图距是18cm，则A、B两地的实际距离是 千米。
2．若a=3，b=5，c=9，且
，则d= 。
3．已知△ABC∽△A′B′C′ ，AB=6，BC=7，AC=8，△A′B′C′的最短边为8，则△A′B′C′的周长是 ；
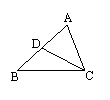
4．如图，△ABC中，D是AB上点，当满足条件 时，△ABC∽△ACD；
5．如果线段c是a、b的比例中项，且a=4，b=9，则c= 。
6．如果点P是线段AB的黄金分割点，且AP>PB，则下列说法
正确的是______（仅填序号）。
①AP2＝PB·AB；②AB2＝AP·PB；
③BP2＝AP·AB；④AP：AB＝PB：AP
7．一个三角形的各边之比为2：5：6，和它相似的另一个三角形的最大边为24，它的最小边为_____。
8．顺次连接三角形三边的中点，所成的三角形与原三角形对应边上中线的比是 哈哈！！！根本难不倒我！
9．在三角形ABC中，D、E分别是AB、AC的中点，则三角形ADE与四边形DEBC面积的比是 。
10．把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩形纸片的长与宽之比为_____。
二、再接再厉（相信你一定找到了足够的宝物，让我们赶快进入下一关。这里有30个宝物，每题3个宝物）
11．下列说法正确的是（ ）
A .所有的等腰三角形都相似 B.所有的直角三角形都相似
C.所有的等腰直角三角形都相似
D.有一个角相等的两个等腰三角形都相似
12．已知ΔABC的三边长分别为
,
,2, ΔA′B′C′的两边长分别是1和
,如果ΔABC与ΔA′B′C′相似,那么
ΔA′B′C′的第三边长应该是( )
A.
B.
C.
D.
13．如图,AB是斜靠在墙上的长梯,梯脚B距墙脚1.6m,梯上点D距墙1.4m,BD长0.55m,则梯子的长为( )
A.3.85m B.4.00m C.4.40m D.4.50m
14．两个相似三角形的相似比是2：3，其中较小的三角形的面积是12，则另一个三角形的面积是（ ）
（A）8 （B）16 （C）24 （D）27
15．若3x－4y = 0，则
的值是（
）
A、
B、
C、
D、
16．下列说法中错误的是( )
A．所有的等腰三角形都相似 B．所有的等边三角形都相似
C．有一对锐角相等的两个直角三角形相似
D．全等的三角形一定相似
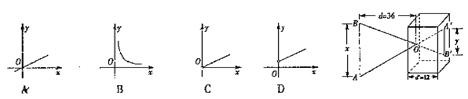
17．(针孔成像问题)根据图中尺寸(AB∥A/B/)，那么物像长y
(A′B′的长)与物长x（AB的长）之间函数关系的图象大致是 （ ）
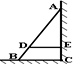
18．如图，D、E分别是△ABC的边AB、AC上的点，∠1＝∠B，AE＝EC＝4，BC＝10，AB＝12，则△ADE和△ACB的周长之比为（ ）
A、 B、 C、 D、
第20题
19．在△ABC与△
中，有下列条件：①
；⑵
③∠A＝∠
；④∠C＝∠
。如果从中任取两个条件组成一组，那么能判断△ABC∽△的共有（ ）组。
A、1 B、2 C、3 D、4
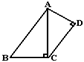
20．如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC∽⊿CAD,只要CD等于( )
A.
B.
C.
D.
三、学以致用（在我们旅游的途中将会遇到许多问题，你能帮我们解决吗？试试看，如能做出来，可有奖励的啊！每解答一个问题可得5个宝物）
21．这是一条有古老传说的河。运用三角形相似的知识，请你设计一个方案测量一条河流的宽度AB（画出示意图，并简要说明理由）．
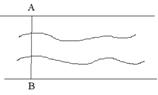
22．如图，AB(底部B不能直接到达)是途中的一个景点，小明想测出塔的高度，于是，小明在点D处测得自己的影长DF=3m，沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.6m，求路灯杆AB的高度.
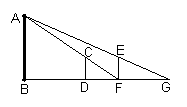
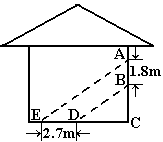
23．中午旅游团将在这里休息，阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.
四、乘胜追击（你就要成功了，让我们乘胜追击，找到最后的宝物每题可得7个宝物）
24．如图,⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
(1)试说明⊿ABD≌⊿BCE.
(2)⊿AEF与⊿ABE相似吗?说说你的理由.
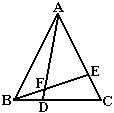(3)BD2=AD·DF吗?请说明理由.
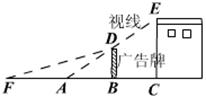
25．如图所示，在房子外的屋檐E处安有一台监视器，房子前有一面落地的广告牌，那么监视器的盲区在△ABD。已知房子上的监视器高3m，广告牌高为1.5m，广告牌距离房子5m，则盲区的长度为多少？
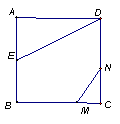
26．如图正方形ABCD的边长为2，AE=EB，线段MN的两端点分别在CB、CD上滑动，且MN=1，当CM为何值时△AED与以M、N、C为顶点的三角形相似？
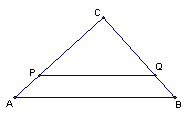
27．如图,已知，在△ABC中,BA=BC=20㎝，AC=30㎝,点P从A点出发,沿AB以4㎝/s的速度向点B运动；同时点Q从C点出发,沿CA以3㎝/s的速度向A点运动,设运动时间为x，
（1）当x为何值时,PQ∥BC；
（2）当S△BCQ∶S△ABC=1∶3时,求S△BPQ∶S△ABC的值；
（3）△APQ能否与△CQB相似,若能,求出AP的长,若不能,请说明理由.
 |
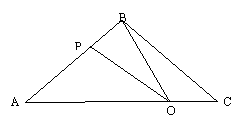28．已知：如图，△ABC，∠C=900，AC=4，BC=3，AB=5。PQ∥AB，点P在AC上（与点A、C不重合），点Q在BC上。
试问：在AB上是否存在点M，使得PQM为等腰直角三角形？若不存在，请简要说明理由；若存在，请求出PQ的长。
阜宁县明达中学命题人：王林 初二数学