初二（上）数学练习卷（十）
班级：____________姓名：_____________学号：____________得分：（1’清洁分）
一、填空题：（2’×16=32’）
1、已知
，则x ：z = ___________________；
2、若a、b互为倒数，则a、b 的比例中项是__________________；
3、当k_____________时，函数y = kx +（2k – 1）x是正比例函数。
4、正比例函数y = mx的图象经过第二、四象限，且经过点P（3 + m，3m + 4），则正比例函数的解析式为__________________；
5、若y与
成正比例，x与z成正比例，则y与z成__________比例；
6、函数
的定义域为__________________；
7、三角形的面积为8平方厘米，这时底边为x厘米，底边上的高为y厘米，则y与x的函数解析式为_____________________；
8、当k = ___________时，函数
是正比例函数；当k = ________时，函数
是反比例函数，且在每个象限内，y随x增大而减小；
9、
二、选择题：
1、函数
的图象过点
（
）
（A）（0，
）； （B）（– 1，1）； （C）（
，
）； （D）（3，）.
2、下列各函数中与函数y = – x相同的是 （ ）
（A）y = – x ； （B）y =
； （C）
； （D） y = 
.
3、下列说法正确的有 （ ）
（1）变量x、y满足x – 3y=1，则y可以是x的函数；
（2）变量x、y满足
，则y可以是x的函数；
（3）变量x、y满足y = – x ，则y可以是x的函数；
（4）变量x、y满足
，则y可以是x的函数.
（A） 0个； （B） 1个； （C） 2个； （D） 3个； （E） 4个.
三、简答题：
1、已知变量x、y与a之间满足关系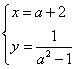
，
求y与x的函数关系及其定义域。
2、已知正比例函数y = ax和反比例函数
的图象有两个交点，如果其中一个交点的横坐标是1，求a及两个交点的坐标。
3、已知等式（x + 1）（y – 2）= 1
（1）求y = f（x）的解析式；（2）写出y = f（x）中自变量x的取值范围；
（3）求f（0）的值；（4）当f（x）= 5时，求x的值。
4、已知
，y1与x – 2成反比例，y2与x + 2成正比例，并且当
时，
；当x = 3时，y =
，求当x = 5时，y的值。
5、如图，在等腰三角形ABC中，AB = AC，A的平分线交BC于D，BC的长为3厘米。动点P从点A出发，以2厘米/秒的速度沿AD移动，出发3秒后到达D，设AP为x厘米，四边形ABPC的面积为y平方厘米，求y与x之间的函数解析式，并求当四边形ABPC是凸四边形时x的取值范围。