初二（上）数学练习卷（十三）
班级：____________姓名：_____________学号：____________得分：（2’清洁分）
一、 填空题：（2’×16=32’）
1． 已知：
，则x = _____________________。
2． 已知
，则
=_______；已知
，则
=___________。
3． 已知y与x2成正比例，且当x = 3时，y = 12，则当y = 4时，x = _______________。
4． 自行车的“牙盘”有32牙，每分钟转120圈，“飞轮”有牙20牙，每分钟转______圈。
5． 命题“等腰三角形底边上的中线与顶角的平分线重合”的逆命题___________________。
6．若等腰三角形的一腰上的高与底边的夹角为20°，那么这个等腰三角形的顶角为______。
7．若函数y=（3 – k）x – k的图象是不经过第一象限的一条直线，则k的取值范围是_________。
8．
的定义域为____________________。
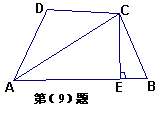
9．如图，在四边形ABCD中，AC平分∠BAD，CE ⊥AB于E，
AE = 
（AD+AB），则∠ADC + ∠ABC 的大小为_________°
10．在△ABC中，已知AB = AC，D在AC上，若∠ABD=2∠DBC，
当△ABD是等腰三角形时，∠A = ____________。
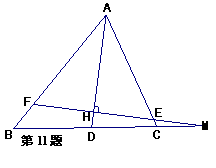
11．在△ABC中，∠BAC = 64°，∠B = 38°，AD平分∠BAC，
M是BC延长线上一点，过M作MF⊥AD，垂足为H，
交AB、AC于F，E，则∠M = _________°
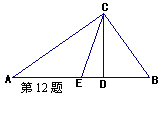
12．在△ABC中，∠ACB = 90°，CD是高，CE是中线，
当BD = 3cm，∠ECD=∠B时，AD = ________________cm。
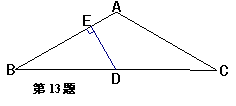13．在△ABC中，AB = AC，∠A = 120°，D为BC的中点，
DE⊥AB于E，则AE ：BE的值为_______________。
14．在△ABC中，∠B和∠C的平分线交于点O，OD⊥BC于点D，
若△ABC的周长为24，OD=3，则△ABC的面积是多少_________________。
15．已知点P（3，7）、Q（5， 11），在x轴上存在一点M，使△MPQ的周长最小，则点M的坐标是______________.
二、选择题：（3’×9=27’）
1．若点A（2，4）在函数y=kx– 2的图像上，则下列各点在此函数图像上的是（ ）
（A）（0，– 2） （B）（
，0） （C）（8，20） （D）（，）
2．已知正比例函数y=（2m–1）x的图象上两点A（x1，y1），B（x2，y2），当x1 ＜x2时，有y1 ＞y2，则m的取值范围是（ ）
（A）
（B）
（C）
（D）
（E）不能确定
3．已知反比例函数y=
的图象上两点A（x1，y1），B（x2，y2），当x1 ＜x2时，
有y1 ＞y2，则m的取值范围是（ ）
（A） （B）
（C） （D） （E）不能确定
4．在下列各式中，y不是x的函数的是（ ）
（A）
（B）
（C）
（D）
5．无论m为何实数，直线
与
的交点不可能在（ ）
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
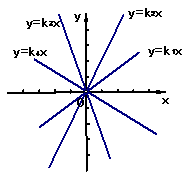
6．根据如图所示的图象，其中比例系数最大的是（ ）
（A）k1 （B）k2 （C）k3 （D）k4
7．下列命题中，假命题是 （ ）
（A）直角三角形三条边的垂直平分线的交点是斜边的中点
（B）经过线段上的一点以及到这条线段两端点距离相等的另一点的直线是这条线段的中垂线
（C）经过角的顶点以及到角两边距离相等的一点的射线是这个角的平分线
（D）等边三角形三条角平分线的交点到三边的距离相等，并且到三个顶点的距离也相等
8．（1）每个命题都有逆命题；（2）每个定理都有逆定理；（3）假命题的逆命题一定是假命题；
（4）定理“直角三角形斜边上的中线等于斜边的一半”有逆定理
以上说法中，正确的个数是 （ ）
（A） 0个 （B） 1个； （C） 2个； （D） 3个 （E） 4个
9．BP和CP是△ABC两个外角的平分线，则∠BPC为 （ ）
（A） 
（B） 90 + （C） 90 –； （D）
三、解答题：（5’×3+6’×4=39’）
1．已知点A（3，m）、B（n，1）在反比例函数
的图象上，直线y = kx + b经过点A、B
求：（1）k、b的值，及直线y = kx + b于x轴的交点C的坐标； （2）△OAB的面积.
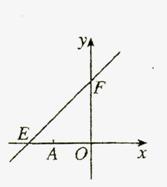2．直线y=kx+6与x轴y轴分别交于点E，F。点E的坐标为（-8，0），点A的坐标为（-6，0）
（1）求k的值；
（2）若点P（x，y）是第二象限内的直线上的一个动点，当点P运动过程中，
试写出△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；
（3）当P运动到什么位置时，△OPA的面积为
，并说明理由。
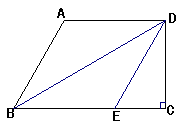3．如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，将直角梯形ABCD沿对角线BD折叠，点A恰好落在BC边上的E点处，若∠A = 120°，AB = 4，求直角梯形ABCD的面积。
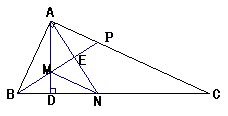4．已知：如图，AD是Rt△ABC斜边BC上的高，∠ABD的平分线交AD于M，交AC于P，∠DAC的平分线交BP于E，交BC于N，
求证：MN∥AC
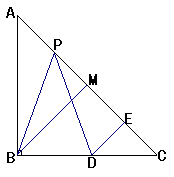5．如图，在等腰直角三角形ABC中，M是斜边AC的中点，P是斜边AC上的一个动点，D是BC边上的一点，且PB = PD，DE⊥AC，垂足为E.
（1）求证：PE = BM；
（2）若AC = 4，AP = x，四边形PBDE的面积为y，
求y与x的函数关系式，并写出自变量x的取值范围。
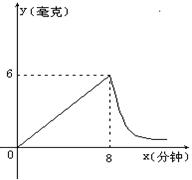
6．为了预防“禽流感”，某学校在教室采用药熏消毒法进行消毒，
已知药物燃烧时，室内每立方米空气中的含药量y（ 毫克）
与时间x（分钟）成正比例，药物燃烧后 ，y与 x 成反比例
（如图所示）。现测得药物8分钟燃烧完毕，此时室内空气中
每立方米的含药量为6毫克，请根据题中提供的信息，
解答下列问题:
（1）药物燃烧时， y关于 x的函数关系式为______________，自变量x的取值范围是
_________________，药物燃烧后，y关于x的函数关系式为__________________
（2）研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过________________分钟后，学生才能回到教室：
（3）研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟，才能有效杀灭空气中的病毒，那么此次消毒有效吗？为什么？
7． 
已知：如图，△ABC中，AB边上的高CF、BC边上的高AD与CA边上的高BE交于H，
联结EF，AH和BC的中点为N，M
求证：MN是线段EF的中垂线。