第二讲 轴对称图形 全等三角形
姓名___________学校____________
1在线段、射线、直线、角、直角三角形、等腰三角形中是轴对称图形的有（ ）。
（A）3个 （B）4个 （C）5个 （D）6个
2、已知直角三角形中30°角所对的直角边为2㎝，则斜边的长为（ ）（A）2 ㎝ （B）4 ㎝ （C）6 ㎝ （D）8㎝
3、点M（1，2）关于原点对称的点的坐标为（ ）（A）（—1，2） （B）（－1，－2） （C）（1，－2） （D）（2，－1）
4、下列说法正确的是( )A．等腰三角形的高、中线、角平分线互相重合B．顶角相等的两个等腰三角形全等
C．等腰三角形一边不可以是另一边的二倍D．等腰三角形的两个底角相等
5、已知∠AOB=30°，点P在∠AOB的内部，P1与P关于OB对称，P2与P关于OA对称，
则P，P1，P2三点构成的三角形是（ ）A．直角三角形 B．钝角三角形 C．等腰三角形 D．等边三角形
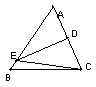6、如图，DE是
ABC中AC边的垂直平分线，若BC=8厘米，AB=10厘米，则EBC的周长为（ ）厘米
A．16 B．28 C．26 D．18
7、等腰三角形的两边长是6和3，周长为______________________。
8、等腰三角形一个角为50°，则此等腰三角形顶角为________________________。
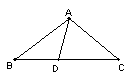
9、在△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A= °。
10、等腰三角形一腰上的中线把这个三角形的周长分成15㎝和12㎝，则这个三角形的底边长为 ㎝。
11．腰长为12㎝，底角为15°的等腰三角形的面积为 。
12．到三角形各顶点距离相等的点是三角形 的交点。
13．在直角坐标系内有两点A(-1，1)、B(2，3)，若M为x轴上一点，且MA+MB最小，则M的坐标是________，MA+MB=________。
14.已知，如图ΔABC中，AB＝AC,D点在BC上，且BD＝AD，DC＝AC.将图中的等腰三角形全都写出来.并求∠B的度数.
15、如图，已知直线MN与MN同侧两点A、B求作：点P，使点P在MN上，且∠APM＝∠BPN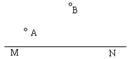 
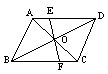16、如图，在⊿ABC中，∠ACB=90，DE是AB的垂直平分线，∠CAE：∠EAB=4：1．求∠B的度数．
1. 两个三角形只有以下元素对应相等，不能判定两个三角形全等的是（ ）
A. 两角和一边 B. 两边及夹角 C. 三个角 D. 三条边
2.下列各图中，不一定全等的是（ ）A．有一个角是45°腰长相等的两个等腰三角形
B. 周长相等的两个等边三角形 C. 有一个角是100°，腰长相等的两个等腰三角形
D. 斜边和和一条直角边分别相等的两个直角三角形。
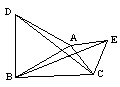
3.如图，AB∥CD，AD∥BC，OE=OF，则图中全等三角形的组数是（ ）A. 3 B. 4 C. 5 D. 6
4.在⊿ABC和⊿A/B/C/中，AB=A/B/，∠A=∠A/，若证⊿ABC≌⊿A/B/C/还要从下列条件中补选一个，
错误的选法是（ ） A. ∠B=∠B/
B. ∠C=∠C/ C. BC=B/C/， D. AC=A/C/，
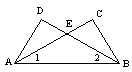
5、如图在△ABD和△ACE都是等边三角形，则ΔADC≌ΔABE的根据是（ ）
A. SSS B. SAS C. ASA D. AAS
6、如图，∠1=∠2，∠C=∠D，AC、BD交于E点，下列结论中不正确的是（
）
A. ∠DAE=∠CBE B. CE=DE C.ΔDEA不全等于ΔCBE D.ΔEAB是等腰三角形
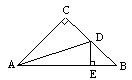
7、如图在ΔABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB=6cm，则ΔDBE的周长是（ ）A. 6cm B. 7cm C. 8cm D. 9 cm
8、等腰
的顶角为
，腰长为10，则底边上的高AD=__________。
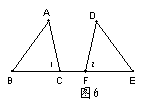
9．如图6，点C、F在BE上，∠1=∠2，BC=EF。请补充条件：__________(写一个即可)，使ΔABC≌ΔDEF。
10如图幼儿园的滑梯中有两个长度相等的梯子（BC=EF），左边滑梯的高度AC等于右边滑梯水平方向的长度DF，则∠ABC+∠DFE= °.
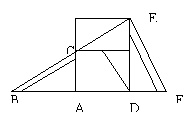
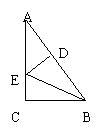11.在RtΔA BC中,BE平分∠ABC,ED⊥AB于D,若AC=3㎝,则AE+DE= ㎝.
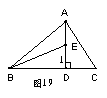12、如图，AD⊥BC于D，AD=BD，AC=BE。
(1) 请说明∠1=∠C
(2) 猜想并说明DE和DC有何特殊关系？
13．如图，在
中，
，
于D，
，求
的长。
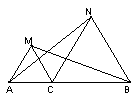14．如图，已知点C是AB上一点，ΔACM、ΔCBN都是等边三角形。
(1) 说明AN=MB
(2) 将ΔACM绕点C按逆时针旋转180°，使A点落在CB上，
请对照原题图在右图画出符合要求的图形。
(3) 在(2)所得到的图形中，结论“AN=BM”是否成立？若成立，
请说明理由；若不成立，也请说明理由。
(4)
在(2)所得到的图形中，设AM的延长线与BN相交于点D，
请你判断ΔABD的形状，并说明你的理由。
15：如图，小明在完成数学作业时，遇到了这样一个问题，AB=CD，BC=AD，请说明：
∠A=∠C的道理，小明动手测量了一下，发现∠A确实与∠C相等，但他不能说明其中的道理，你能帮助他说明这个道理吗？试试看。
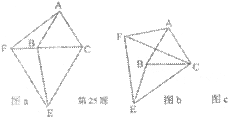16、如图a，⊿ ABC和⊿CEF是两个大小不等的等边三角形，且有一个公共顶点C，连接AF和BE. (1)线段AF和BE有怎样的大小关系?请证明你的结论；
(2)将图a中的△CEF绕点C旋转一定的角度，得到图b，(1)中的结论还成立吗?作出判断并说明理由；
(3)若将图a中的△ABC绕点C旋转一定的角度，请你画山一个变换后的图形c(草图即可)，(1)中的结论还成立吗?作出判断不必说明理由；
(4)根据以上证明、说理、画图，归纳你的发现.
17.如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.
|
|
|
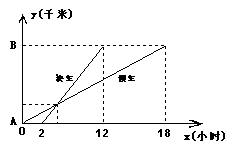
18．一慢车和一快车沿相同路线从A地到相距120千米的B地，
|
|
|
⑴慢车比快车早出发 小时，快车比慢车少用 小时到达B地；
|
|