三角形全等的判定(SSS、SAS)
一、填空题
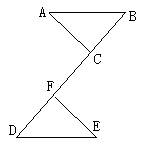
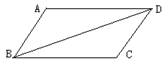1、如图，AB=CD，AD=CB，则△ABD和△CDB的关系是__________，AB与CD的位置关系是___________。
2、已知：△ABC的△DEF中，AB=DE，BC=EF，AC=DF，∠B=50º，∠C=70º，则△ABC_____△DEF,∠D=_______。
3、在△ABC和△DEF中，AB=4，BC=5，AC=6，DF=5，当DE=______时，△ABC≌△EFD。
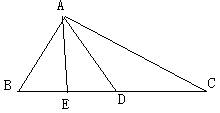
4、如图，AD=AB，BC=DC，DE=2，∠AED=110º，则BE=________º，∠BEC=_______º。
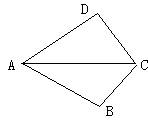
5、如图，AB=DE，AC=DF，则还需添加条件：__________（只要写出其中一个），可证△ABC≌△DEF。
6、如图，AB=DE，AC=EF，DC=BF得BC=_________，从而根据__________证得△ABC≌△___________。
7、如图，CD是△ABC的中线，我们常把CD延长一倍到E，即DE=CD，连结AE，可得到△ADE≌△________，理由是_________，实际上△ADE是由△BDC旋转_________度后得到的。
8、如图，△ABC和△ADC中，AD=AB，若添加条件_________或_________，可证得△ABC≌△ADC，理由是_________或_________。
二、选择题
9、下列说法不正确的是（）
A、全等三角形对应边上的高相等
B、全等三角形对应边上的中线相等
C、全等三角形对应角的角平分线相等
D、全等三角形对应边上的垂直平分线相等
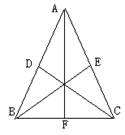
10、等腰△ABC中，AB=AC，D、E、F分别是AB、AC、BC的中点，图中全等三角形共有（）
A、5对 B、6对 C、7对 D、8对
11、下列说法正确的是（）
A、有两边及其中一边的对角对应相等的两个三角形全等
B、两个等边三角形全等
C、各有一个角是40º的两个等腰三角形全等
D、三条边对应相等的两个三角形的三个角也对应相等。
12、两个三角形的两边及其中一边的对角线对应相等，那么下面说法：
（1）这两个三角形总不能全等；（2）相等的角不是直角时两个三角形全等；
（3）相等的角是直角时两个三角形全等。
其中说法正确的个数有（）
A、0个 B、1个 C、2个 D、3个
13、下面给出四个命题：
（1）腰和顶点对应相等的两个等腰三角形全等
（2）两条直角边对应相等的两个直角三角形全等
（3）等腰三角形底边上的中线把这个等腰三角形分成两个全等的三角形
（4）直角三角形斜边上的中线把这个直角三角形分成两个全等的三角形
A、1个 B、2个 C、3个 D、4个
14、如图，△ABD和△ACE都是等边三角形，那么△ADC≌△ABE的根据是（）
A、SSS B、SAS C、ASA D、AAS
15、下列命题：
（1）边长相等的两个等边三角形全等
（2）三角对应相等的两个三角形全等
（3）在△ABC和△A’B’C’，若AB=BC=CA，A’B’=B’C’=C’A’。则△ABC≌△A’B’C’
（4）腰长相等，且有一个角为100º的两个等腰三角形相等
其中真命题共有（）
A、1个 B、2个 C、3个 D、4个
16、如果只有一条边相等的两个三角形全等，那么这两个三角形必须是（）
A、等腰三角形 B、等腰直角三角形 C、等边三角形 D、直角三角形
17、若两个三角形全等，则
（1）对应边相等；（2）对应角相等；（3）对应中线相等；（4）对应角平分线相等；（5）周长相等；（6）面积相等。
上述结论中正确的结论个数有（）
A、3个 B、4个 C、5个 D、6个
18、有两边和其中一边上的中线对应相等的两个三角形（）
A、一定全等 B、一定不全等 C、不一定全等 D、形状相同但不全等
三、解答题
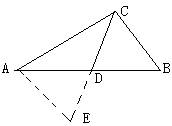
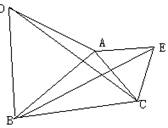
19、如图，AB=DE，AC=DF，BF=CE。求证：AB∥DE。
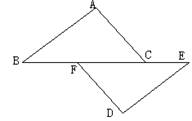
20、如图，AB=CD，AC=BD，求证：∠B=∠C。
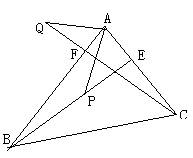
21、如图，△ABC中，BE、CF是高，BP=AC，CQ=AB，试问：AP与AQ有怎样的关系，并证明你的结论。
22、如图，AE⊥AD，AB⊥AF，AE=AD，AF=AB，AD∥BC，AD=BC。求证：AC、EF。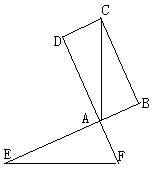
23、如图，AB=AC，BE=CE。求证：（1）AE平分∠BAC；（2）AD垂直平分BC。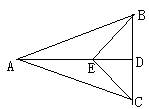
24、如图，AB=AE，BC=ED，∠B=∠E，F为CD的中点。求证：AF⊥CD。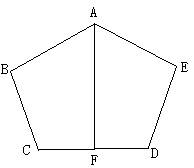
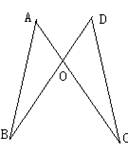
25、如图，BC=BD，AC=AD，AB与CD交于点O。求证：AB⊥CD。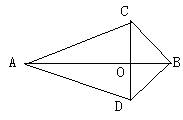
26、如图，AB=AC，BD、CE交于F，BF=CF。求证：∠AFE=∠AFD。
27、如图，△ABC中，D是BC上一点，CD=AB，AE是△ABD的中线，且AC=2AE。求∠CAE的平分线。（提示：延长AE到F，使EF=AE，连结FD） 