八年级数学（上）期末检测题
一.选择题.（本题共8小题，共32分） 班别： 姓名：
1、函数y=
中，字母的取值范围是（ ）
Ａ、a<1 Ｂ、a≤1 Ｃ、a≥1 Ｄ、a>1
2、下列计算正确的是（ ）
（A）
（B）
（C）
（D）
3、将直线
向上平移两个单位，所得的直线是（ ）
A．
B．
C．
D．
4、在直角坐标系中，A（1，2）点的横坐标乘以－1，纵坐标不变，得到A’点，则A与A’的关系是（ ）
A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、将A点向x轴负
5．下列图案是轴对称图形的有（ ）。
（A）1个 （B）2个 （C）3个 （D）4个
 |  |  | |||||
 | |||||||
第6题
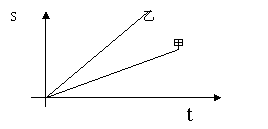
6、如图，射线甲、乙分别表示甲、乙两车所走路程与时间的关系图，则两车速度关系是：( )
A 、 甲比乙快 ； B 、乙比甲快 ； C 、 甲乙同速 ； D 、不能判断。
7．将写有字“B”的字条正对镜面，则镜中出现的会是（ ）。
（A）B
（B） （C） （D）
8、已知直角三角形中30°角所对的直角边为2㎝，则斜边的长为（ ）
（A）2 ㎝ （B）4 ㎝ （C） 6 ㎝ （D）8㎝
9、点M（1，2）关于原点对称的点的坐标为 （ ）
（A）（—1，2） （B）（－1，－2） （C）（1，－2） （D）（2，－1）
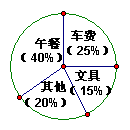
11、小明把自己一周的支出情况，用如图所示的统计图来表示，下面说法正确的是（ ）
A． 从图中可以看出具体的消费数额； B.从图中可以直接看出各项消费额占总消费额的百分比；
C.从图中可以看总消费数额； D.从图中可以看出各项消费额在一周的具体变化情况。
12、若
，则x的取值是（ ）
（A）
（B）x≥—
(C) x＞— （D）x≠
二、填空题（本题共8题，共32分）
1、分解因式：ab2－2a＝_________. 腰长为12㎝，底角为15°的等腰三角形的面积为 。
2、等腰三角形一个底角为50°，则此等腰三角形顶角为____________。
3、点A(2，4)在正比例函数的图象上，这个正比例函数的解析式是
4、把一组64个数据的样本分成8组，从第一组到第四组的频数分别为5、7、11、13，第五组到第七组的频率都是0．125，则第八组的频率为
。
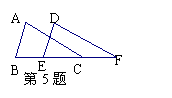
5、如图，已知∠ABC=∠DEF，AB=DE，要说明ΔABC≌ΔDEF若以“SAS”为依据，
还要添加的条件为___________；
6、在△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A= °。
7、在Rt⊿ABC中，∠C=90°，∠A=30°，AB=12，则BC= 。
8、若4x2－kxy+y2表示一个完全平方式，则k=
9、直线
可由直线向
平移 得到。
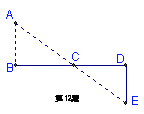
10、如图所示：要测量河岸相对的两点A、B之间的距离，先从B处出发与AB
成90°角方向，向前走50米到C处立一根标杆，然后方向不变继续朝前走50米
到D处，在D处转90°沿DE方向再走17米，到达E处，使A、C与E在同一直线上，那么测得A、B的距离为_____米。
三、解答题（本题5题，共36分）
1、计算： (1)2(m＋1)2－(2m＋1)(2m—1) (2)4x2－(2－x＋3)(－2x－3).
2、因式分解：(1)2x2y3－8x4y5 (4) a2－6a＋9－b2．
3、先化简，再求值： (2a－3b)2－(3b＋2a)2，其中a＝－，b＝3．
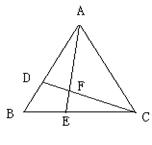4．如图，在△ＡＢＣ中，点Ｄ在ＡＢ上，点Ｅ在ＢＣ上，ＢＤ＝ＢＥ。请你再添加一个条件，使得△ＢＥＡ≌△ＢＤＣ，并给出证明。
你添加的条件是：___________
证明：
5、下面的方格纸中，画出了一个“小猪”的图案，已知每个小正方形的边长为1．
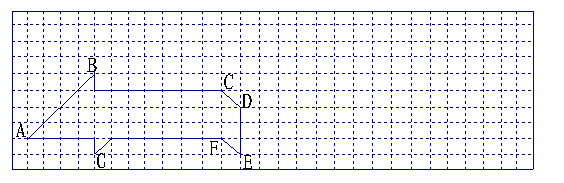
（1）“小猪”所占的面积为多少？
（2）在方格纸中作出“小猪”关于直线DE对称的图案（只画图，不写作法）；
（3）以G为原点，GE所在直线为x轴，GB所在直线为y轴，小正方形的边长为单位长度建立直角坐标系，可得点A的坐标是（_______，_______）．
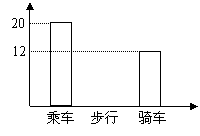6、右图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。
（1）求该班有多少名学生？
（2）补上步行分布直方图的空缺部分；
（3）在扇形统计图中，求骑车人数所占的圆心角度数。
（4）若全年级有500人，估计该年级步行人数。
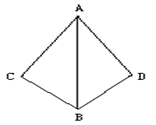7、已知：AB平分∠CAD，AC=AD．求证：BC=BD．
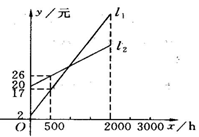
8．如图所示，L1，L2分别表示一种白炽灯和一种节能灯的费用y（费用=灯的售价+电费，单位：元）与照明时间x（h）的函数关系图像，假设两种灯的使用寿命都是2000h，照明效果一样．
（1）根据图像分别求出L1，L2的函数关系式．（2）当照明时间为多少时，两种灯的费用相等？
（3）小亮房间计划照明2500h，他买了一个白炽灯和一个节能灯，请你帮他设计最省钱的用灯方法．
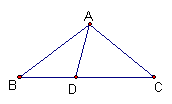9、已知，如图ΔABC中，AB＝AC,D点在BC上，且BD＝AD，DC＝AC.将图中的等腰三角形全都写出来.并求∠B的度数.
 |
10、如图，在⊿ABC中，∠ABC和∠ACB的平分线交于点O，过O点作EF∥BC，交AB于E，交AC于F，BE=5cm，CF=3cm，求EF的长．
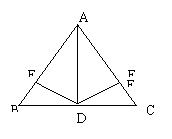11、已知：如图，AD平分∠BAC,DE⊥AB,DF⊥AC，DB=DC，求证：△ABC是等腰三角形。
| |
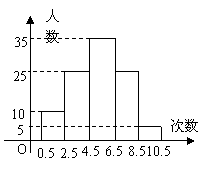12、为了了解某初中学生的体能情况，抽取若干名学生在单位时间内进行引体向上测试，将所得数据整理后，画出频数分布直方图（如图），图中从左到右依次为第1、2、3、4、5组。
（1） 求抽取多少名学生参加测试？
（2） 处于哪个次数段的学生数最多？（答出是第几组即可）
（3） 若次数在5次（含5次）以上为达标，求这次测试的达标率。
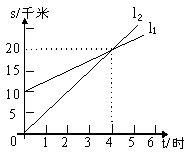13、如图，
反映了甲离开A的时间与离A地的距离的关系，
反映了乙离开A地的时间与离A地的距离之间的关系，根据图象填空：
（1）当时间为2小时时，甲离A地 千米，
乙离A地 千米。
（2）当时间为6小时时，甲离A地 千米，
乙离A地 千米。
（3）当时间 时，甲、乙两人离A地距离相等。
（4）当时间 时，甲在乙的前面，
当时间 时，乙超过了甲。
（5）对应的函数表达式为
，对应的函数表达式为
。
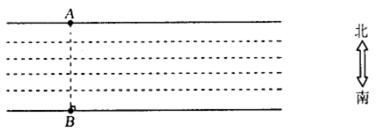
14．一条大河两岸的A、B处分别立着高压线铁塔，如图所示．假设河的两岸平行，你在河的南岸，请利用现有的自然条件、皮尺和标杆，并结合你学过的全等三角形的知识，设计一个不过河便能测量河的宽度的好办法．(要求，画出示意图，并标出字母，结合图形简要叙述你的方案)
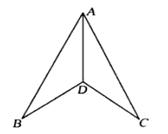
15．如图，在△ABD和△ACD中，已知AB＝AC，∠B＝∠C，求证：AD是∠BAC的平分线．
16．某苹果生产基地组织20辆汽车装运A，B，C三种苹果42吨到外地销售．按规定每辆车只装一种苹果，且必须装满，每种苹果不少于2车．
| 苹果品种 | A | B | C |
| 每辆汽车的装载重量(吨) | 2.2 | 2.1 | 2 |
| 每吨苹果获利(百元) | 6 | 8 | 5 |
(1)设用x辆车装运A种苹果，用y辆车装运B种苹果，不运C种苹果．根据上表提供的信息，求y与x之间的函数关系式，并求出x的取值范围；
(2)设此次外销活动的利润为W(百元)，求W与x之间的函数关系式及最大利润，并制定相应的车分配方案