八年级数学（下）第一次调研试卷
班级 姓名 成绩
一、填空题（每小题2分，共16分）
1．近视眼镜的度数
（度）与镜片焦距
（米）成反比例.已知400度近视眼镜片的焦距为与镜片焦距之间的函数关系式是_____________________．
2．若分式方程
有增根，则m的值是 ．
3．已知反比例函数
，当
时，其图象的两个分支在第二、四象限内．
4．反比例函数的图像经过（－2，6）点、（ａ，－3）及（6，ｂ）点，则ａ＋ｂ＝ ．
5．若分式
有意义，则x
．
6．当x 时，分式
的值为零．
7．化简：
＝
．
8．某商场降价销售一批服装，降价a﹪后的售价为120元，则原销售价是 元．
二、单项选择题（每小题3分，共24分）
9．下列代数式中，是分式的是（ ）
A、
B、
C、
D、
10、下列函数中，y是x的反比例函数是（ ）
A、
B、
C、
D、
11．已知
，则
的值是（ ）
A、-5 B、
12．化简
的结果是（ ）
A、
B、
C、
D、
13．赵强同学借了一本书，共280页，要在两周借期内读完．当他读了一半时，发现平均每天要多读21页才能在借期内读完．他读前一半时，平均每天读多少页?如果设读前一半时，平均每天读x页，则下面所列方程中，正确的是（ ）
A、
B、
C、
D、
14．如果反比例函数
的图像经过点（－3，－4），那么函数的图像应在（ ）
A、第一、三象限 B、第一、二象限 C、第二、四象限 D、第三、四象限
15．在同一直角坐标平面内，如果直线
与双曲线
没有交点，那么
和
的关系一定是（ ）
A、<0，>0 B、>0，<、同号 D、、异号
16．若点（
,
）（
,
）（
,
）都在反比例函数
的图象上，并且＜0＜＜，则下列各式正确的是（ ）
A、＜＜ B、＜＜ C、＜＜ D、＜＜
三、按要求解答下列各题（共32分）
17．（6分）化简：
，并选一个你喜爱的且使原式有意义的值代入求值．
18．（6分）解分式方程：
19．（10分）为加快西部大开发，某自治区决定新修一条公路，甲、乙两工程队承包此项工程．如果甲工程队单独施工，则刚好如期完成；如果乙工程队单独施工就要超过6个月才能完成，现在甲、乙两队先共同施工4个月，剩下的由乙队单独施工，则刚好如期完成。问原来规定修好这条公路需多长时间？
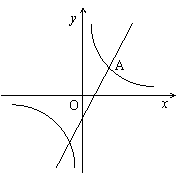20．（10分）如图，已知反比例函数和一次函数
的图象相交于第一象限内的一点A（1，n）．
（1）求A点的坐标以及反比例函数、一次函数的关系式；
（2）若两图象在第三象限的交点的纵坐标为
，问当x取
何值时，一次函数的值大于反比例函数的值？
四、探索研究题（共28分）
21．如图①，已知矩形ABCD的顶点A在原点，顶点C在反比例函数的图象上，AB、AD分别在两坐标轴上，且
，
．
（1）求反比例函数的关系式；（2分）
（2）求顶点C的坐标；（2分）
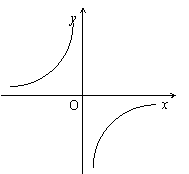
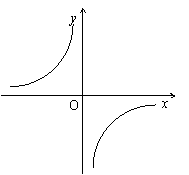
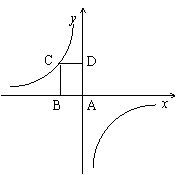（3）是否还存在其它符合题意的矩形？如果有，请你画出示意图（可以画在图①中，也可以画在图②或③中），并直接写出C点的坐标；如果没有，请你说明理由．（4分）
图① 图② 图③
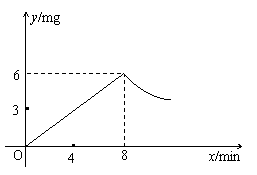
22．为了预防“非典”，某学校对教室采用药熏进行消毒．已知药物燃烧时，室内每立方米的空间含药量y(mg)与时间x(min)成正比例．药物燃烧完毕后，室内每立方米的空间含药量y与时间x成反比例，它们之间的函数关系如图所示．现测得药物8min燃毕，此时室内空气中每立方米的含药量为6mg．请根据题中所提供的信息，解决下列问题：
（1）药物燃烧时，y与x的函数关系式，并指出自变量x的取值范围；（4分）
（2）药物燃烧后，y与x的函数关系式；（2分）
（3）研究表明，当空气中每立方米的含药量低于3mg时，学生才可以进教室，那么从消毒开始，至少需要经过多长时间后，学生才能回到教室？（2分）
（4）研究表明：当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能有效杀灭空气中的病菌，那么这次消毒是否有效，为什么？（4分）
 |
23．阅读材料：方程
－
=
－
的解为x=1，
方程－
=－
的解为x=2，
方程－=－
的解为x=3，…
（1）请你观察上述方程与解的特征，写出一个解为5的分式方程．（3分）
（2）写出能反映上述方程一般规律的方程，并直接写出这个方程的解．（5分）