八年级数学
第二学期期中检测
亲爱的同学：本场考试用时90分钟，时间充足，愿你放松心情，认真审题，缜密思考，细心演算，交一份满意的答卷。
一、细心选一选（每题3分，共30分）
1、要使
有意义，则x的取值范围为………………………………………（ ）
A、x＝1 B、x＜1 C、x≥1 D、x≤1
2、下列各方程中，是一元二次方程的是…………………………………………（ ）
A、3x＋2＝3 B、x3＋2x＋1＝0 C、x2＝1 D、x2＋2y＝0
3、在频数分布表中，各组的频率之和等于………………………………………（ ）
A、1 B、2 C、3 D、4
4、方程x2＝x的解是………………………………………………………………（ ）
A、x＝1 B、x＝0 C、x1＝0，x2＝1 D、x1＝0，x2＝－1
5、下列命题中，真命题是…………………………………………………………（ ）
A、有一个角为60°的三角形是等边三角形 B、全等三角形的对应边相等
C、如果a2＝b2，那么a＝b D、两锐角的和是锐角
6、若m是一元二次方程x2＋x－5＝0的一个解，则m2＋m＋2的值为（ ）
A、－3 B、7 C、－7 D、不存在
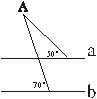
7、如图，直线a∥b，则∠A＝ 度。………（ ）
|
8、用配方法解方程x2＋4x＝－1，经配方后得到………（ ）
A、（x＋2）2＝5 B、（x－2）2＝3
C、（x＋2）2＝3 D、（x－2）2＝5
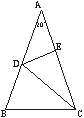
9、如图，△ABC中，AB＝AC，∠A＝20°，DE垂直平分AC，
则∠BCD的度数为（ ）
|
10、某超市失窃，大量的商品在夜间被窃贼用汽车运车，三个嫌疑人
被警方传讯，已知警察已掌握了三个事实：（1）罪犯不在甲、乙、丙三人之外；
（2）丙作案时总得有乙跟随；（3）甲不会开车。在此案中，一定有参与作案
的对象是（ ）
A、甲 B、乙 C、丙 D、乙和丙
二、认真填一填（每题3分，共30分）
11、化简：
＝
。
12、6位同学分别对数学课本的厚度进行了目测，得到了以下数据（单位：cm）1.0、0.9、0.8、1.2、1.3、0.7，则这组数据的极差是 cm。
13、规定一种新的运算“*”，对于任意实数x，y，满足x*y＝x2－y2，则按此规定，2*
＝
。
14、把命题“有三边对应相等的两个三角形全等”改写成“如果……那么……”的形式，可写为 。
15、对于一元二次方程x2―2x―1＝0，若a、b、c分别为二次项系数，一次项系数，常数项，那么b2－4ac的值为 。
16、已知：三条直线l1、、l2、、l3 。其中l1∥l2，l2∥l3，求证：l1∥l3，若用反证法证明该题，第一步应假设 。
17、请写出一条可以判断两个角相等的定理： 。
18、方程（m2－1）x2＋mx－1＝0是关于x的一元二次方程，则m满足的条件是 。
19、近年来，我市开展了“社会主义新农村建设”活动并取得了明显成效，下面是市长和市民的一段对话。
市长：全市在2006年已有“新农村建设达标村”100个，计划到2008年全市“新农村建设达标村”要达到196个。
市民：市长，按这个计划，从2006年到2008年平均每年“新农村建设达标村”增长率是多少？
根据以上对话，设2006年到2008年平均每年“新农村建设达标村”的增长率为x，则可列出方程
，（只列方程，无需求解）。
20、珍珍同学收藏了一枚等腰三角形形状的邮票，经测量该枚邮票的腰长2cm，底角为30°，则该枚邮票的面积为 cm2。
三、用心解一解（本题有5题，共40分）
21、计算（本题8分）
|
|
－
＋2
（2）1＋（－
）（＋）
22、解下列方程（本题8分）
（1）2（x－4）2＝18 （2）x2－6x－16＝0
解： 解：
23、（本题6分）
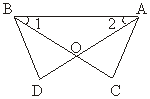
如图，△ABC与△BAD中，AD与BC相交于O点，∠1＝∠2，请你添加一个条件（不再添加其它线段，不再标注或使用其他字母），使AC＝BD，并给出证明。
你添加的一个条件是
证明：
24、（本题8分）龙港学区某中学在今年的校园科技节中举行了八年级科技知识竞赛，李老师将参赛学生的成绩（得分均为整数，满分为100分）进行整理后，分成五组，绘制了下面的频数分布直方图，已知图中从左到右的第一，第二，第四，第五小组的频数分别是30，40，10，5，且第一小组的频率为0.30，请你帮助李老师完成下列问题。
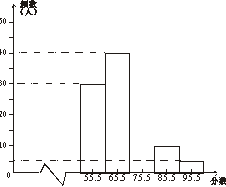（1）本次参赛的学生总人数是
人。
（2）补全这个频数分布直方图。
（3）参赛学生成绩的中位数落在第 小组内。
（4）若成绩在70分以上（不含70分）的学生就能获奖，
则这次比赛的获奖率为 。
25、（本题10分）
龙港某商场购进一种单价为40元的篮球，如果以单价50元出售，那么每月可售出400个，根据销售经验，售价每提高1元，每月销售量相应减少10个。
（1）（2分）假设销售单价提高x元，那么销售每个篮球所获得的利润是 元；这种篮球的销售量是 个，（以上两个空格均用含x的代数式表示）.
（2）（4分）若要使每月销售的利润达到6000元，此时每个篮球的售价应定为多少元？
解：
（3）（4分）6000元是否为每月销售篮球的最大利润？如果是，请说明理由。如果不是，那么每月的最大利润为多少元，此时每个篮球的售价应定为多少元？
（“每月的最大利润”、“此时每个篮球的售价”均可直接写出答案，无需书写解题过程）。
解：
（祝贺你顺利完成本卷，现在请你对考试中存在的疑惑，进行仔细检查思考，祝你成功！）