2
第四章 相似图形单元测试(北师大版)
考试用时90分钟,满分100分
2006年4月20日 石抱柱
班级:________ 姓名:________
| 题号 | 一 | 二 | 三 | 四 | 五 | 总分 |
| 分数 |
|
|
|
|
|
|
一、填空题(20分,每小题4分)
1. 两个相似三角形的最短边分别是9 cm和6 cm,它们的周长和是60 cm,则大三角形的周长=______________cm,小三角形的周长=______________cm.
2.如果两个相似三角形对应高的比为4∶5,那么这两个相似三角形的相似比为____________;对应中线的比为____________;对应角平分线的比为____________;对应周长的比为____________;对应面积的比为____________.
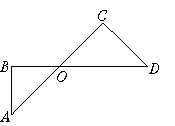
图4-70
3.如图4-70,线段AC、BD相交于点O,要使△AOB∽△DOC,应具备条件______________,还需要补充的条件是______________或______________或______________.
4. 如果线段a、b、c、d是成比例线段且a=3,b=4,c=5,则d=______________;
5.已知线段a,b,d,c成比例,a=3cm,b=2cm,c=6cm则d= cm
二、选择题 (20分,每小题4分)
1.两地实际距离是500 m,画在图上的距离是25 cm,若在此图上量得A、B两地相距为40 cm,则A、B两地的实际距离是( )
A.800 m B.8000 m
C.32250 cm D.3225 m
2.Rt△ABC中,CD是斜边AB上的高,该图中共有x个三角形与△ABC相似,x的值为( )
A.1 B.2
C.3 D.4
3.下列各组三角形中,相似的为( )
A.△ABC中,∠A=35°,∠B=50°
△A′B′C′中,∠A′=35°,∠C′=105°
B.△ABC中,AB=1.5,BC=1.25,∠B=38°
△A′B′C′中,A′B′=2,B′C′=![]() ,∠B′=38°
,∠B′=38°
C.△ABC中,AB=12,BC=15,AC=26
△A′B′C′中,A′B′=20,B′C′=25,C′A′=40
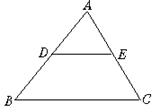
图7-71
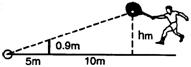 4、已知:如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,则球拍击球的高度h
应为( )
4、已知:如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,则球拍击球的高度h
应为( )
A、0.9m B、1.8m C、2.7m D、6m
5、两相似三角形的周长之比为1:4,那么他们的对应边上的高的比为( )A、1:2 B、![]() :2 C、2:1 D、1:4
:2 C、2:1 D、1:4
三、解答题(16分)
1.(8分)如图4-71,已知△ADE∽△ABC,AD=3 cm,DB=3 cm,BC=10 cm,∠A=70°、 ∠B=50°.
求:(1)∠ADE的度数;
(2)∠AED的度数;
(3).DE的长
. 2、(8分)若a、b、c为△ABC的三边,且满足a2+b2+c2-ab-bc-ca=0。探索△ABC的形状,并说明理由。
四、说理题:(20分)
![]() 1、(10分)如图,点P是 ABCD的边BC延长线上一点,AP分别交BD、CD于点M、N,请你写出图中的相似三角形,不要遗漏哦!
1、(10分)如图,点P是 ABCD的边BC延长线上一点,AP分别交BD、CD于点M、N,请你写出图中的相似三角形,不要遗漏哦!

2、(10分)如图,已知:DE∥BC,DF∥AC,AD=6,BD=4,DE=7,
(1)
 试说明:△ADE∽△DBF;
试说明:△ADE∽△DBF;
(2) 求线段BF的长。
五、附加题:(每小题10分,共20分)
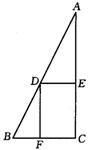
1、巳知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8.点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF.
设DE=x,DF=y.
⑴求y与x之间的函数关系式,并求出x的取值范围;
⑵设四边形DECF的面积为s,求S与x之间的函数关系式,并求出s的最大值.
2、操作题:在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角尺的直角顶点与点P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.
探究:(1)观察操作结果,哪一个三角形与△BPC相似?并证明你的结论;
 (2)当点P位于CD的中点时,你找到的三角形与△BPC的周长比是多少?
(2)当点P位于CD的中点时,你找到的三角形与△BPC的周长比是多少?