一次函数(四)
班级：__________ 姓名：____________ 学号：____________ 成绩：____________
一、填空题。（每空3分，共54）
1.
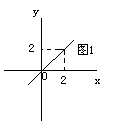
如图（1），在直角坐标系中，直线
所表示的函数是_______
2.
函数
中，自变量
的取值范围是__________。
3.
函数
是正比例函数，则
__________，
随的增大而__________。
4.
正比例函数图象经过两点A（
，4）B（4，
），则__________。
5.
函数
与轴交点坐标为__________，与轴交点坐标为__________,通过第__________象限，它与两坐标轴围成三角形面积为__________.
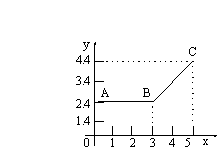6、如图2直线ＡＢＣ为甲地向乙地打长途电话所需付的话费ｙ（元）与通话时间ｔ（分钟）之间的函数关系的图象，当ｔ≥3时，该图象的解析式为 ；从图象可知，通话2分钟需付电话费为 元；通话7分钟需付电话费 元.
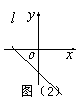
图2
7、y－2与x成正比例，当x=2 时，y=4 ，则x= _______时，y=－4 ．
8、已知y 与3x 成正比例，且当x=8 时，y=12 则y 与x 的函数解析式
9、已知一次函数y=kx+5的图象经过点（-1，2），则k= .
10、某商店出售一种瓜子，其售价y（元）与瓜子质量x（千克）之间的关系如下表
| 质量x（千克） | 1 | 2 | 3 | 4 | |
| 售价y（元） | 3.60+0.20 | 7.20+0.20 | 10.80+0.20 | 14.40+0.2 |
由上表得y与x之间的关系式是 .
11、已知函数y=(2m+1)x+m –3 (1)若函数图象经过原点,则m=
(2)若这个函数是一次函数,且y随着x的增大而减小,则m的取值范围 .
二、选择题。（每小题4，共12）
12、下列不是一次函数的是（ ）。
A．
B．
C．
D．
13、如图（3）线是一次函数
的图象，则有（ ）。
A．
、
B．、
C．
、 D．、
.14、已知一次函数y=ax+4与y=bx-2的图象在x轴上相交于同一点,则 
的值是(
)
(A)4 (B)-2 (C) 2 (D)- 4
三、（第15题7分，16、17、18题9分共34分）
15、已知y与－2成正比例，且
时，
。
（1）求出与之间的函数关系式；（5分） （2）当
时，求的值。（2分）
16、已知一次函数y=kx+b的图象经过点(-1, -5),且与正比例函数y= x的图象相交于点(2,a),
求 (1)a的值 (2)k,b的值 (3)这两个函数图象与x轴所围成的三角形面积.
.
17、为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9、10月份的用水量和所交水费如下表所示:
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
设某户每月用水量x(立方米),应交水费y(元) (1) 求a,c的值
(2) 当x≤6 , x＞6时,分别写出y于x的函数关系式
(3) 若该户11月份用水量为8立方米,求该户11月份水费是多少元?
18.某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料生产A、B两种产品，共50件．已知生产一件A种产品需用甲种原料9千克，乙种原料3千克，可获利润700元；生产一件B种产品，需用甲种原料4千克，乙种原料10千克，可获利润1200元．设生产A、B两种产品获总利润为y(元)，其中A种的生产件数为x，试写出y与x之间的函数关系式。