第十九章解直角三角形(综合)
班级 姓名 得分
一、选择题(每题3分,共24分)
1.一个直角三角形,两直角边长分别为3和4,下列说法正确的是 ( )
(A)斜边长为25 (B)三角形的周长为25
(C)斜边长为5 (D)三角形面积为20
2.在Rt△ABC中,∠C=900,若AB=2AC,则cosA= ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() 。
。
3.小丰妈妈买了一部29英寸(74cm)电视机,下列对29英寸的说法中正确的是 ( )
(A) 小丰认为指的是屏幕的长度
(B)小丰的妈妈认为指的是屏幕的宽度
(C)小丰的爸爸认为指的是屏幕的周长
(D)售货员认为指的是屏幕对角线的长度
4.下列结论错误的是 ( )
(A)三个角度之比为1∶2∶3的三角形是直角三角形;
(B)三条边长之比为3∶4∶5的三角形是直角三角形;
(C)三条边长之比为8∶16∶17的三角形是直角三角形;
(D)三个角度之比为1∶1∶2的三角形是直角三角形。
5.若∠A为锐角,且cosA=![]() ,则有
( )
,则有
( )
(A)00<∠A<300 (B)300<∠A<450 (C)450<∠A<600 (D)600<∠A<900。
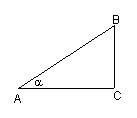 6.如图,为测楼房BC的高,在距楼房30米的A处,测得楼顶B的仰角为α,则楼房BC的高为
( )
6.如图,为测楼房BC的高,在距楼房30米的A处,测得楼顶B的仰角为α,则楼房BC的高为
( )
(A)![]() 米(B)
米(B)![]() 米 (C)
米 (C)![]() 米 (D)
米 (D)![]() 米
米
7.一般情况下,测量楼高的最佳方法是 ( )
(A)站在楼顶望地面两点,测得这两点的俯角,再量得这两点的距离,进行计算.
(B)在地面上任取两点,测得这两点向上望的仰角,再测得这两点的距离,进行计算.
(C)在地面上选适当的一点,使它与楼顶的仰角为300,再测量该点到楼底的距离,利用特殊值进行计算.
(D)在地面上选适当的一点,使它与楼顶的仰角为450,只需测量该点到楼底的距离便求出楼高.
8.男孩戴维是城里的飞盘冠军,戈里是城里最可恶的踩高跷的人,两人约定一比高低.戴维直立肩高1米,他投飞盘很有力,但需在13米内才有威力;戈里踩高跷时鼻子离地13米,他的鼻子是他惟一的弱点.戴维需离戈里( )远时才能击中对方的鼻子而获胜.
(A) 7米 (B)8米 (C) 6米 (D)5米
二、填空题(每题4分,共28分)
9.已知甲往东走了4km,乙往南走了3km,这时甲、乙俩人相距 。
10.直角三角形的三边长为连续偶数,则其周长为 。
11.在RtΔABC中,![]() b+c=6,则b=_________.
b+c=6,则b=_________.
12.已知![]() ,则由此
,则由此![]() 为三边的
为三边的
三角形是 三角形.
13.已知等腰三角形的两边分别为4㎝,5㎝,则此等腰三角形底角的正切值为__________.
14.计算(tan30°-1)+cot60°-1=______。
![]() ________
________
15.等腰△ABC中,AB=AC=17cm,BC=16cm,则BC边上的高AD=_______。
三、解答题(共48分)
16.(6)要登上8m高的建筑物,为了安全需要,需使梯子底端离建筑物6m,至少需要多长的梯子?
17. (6)一个三角形的三边长的比为3:4:5,那么这个三角形是直角三角形吗,为什么?
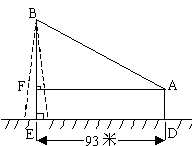
18.(8)如图,在离铁塔93米的A处,用测角器测得塔顶的仰角为∠BAF,已知测角器高AD=1.55米,若∠BAF=30°,求铁塔高BE。
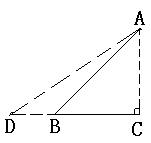 19.(8)如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45o,为了提高该堤的防洪能力,现把它改成坡比为
19.(8)如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45o,为了提高该堤的防洪能力,现把它改成坡比为![]() 的斜坡AD. 求DB的长(结果保留根号).
的斜坡AD. 求DB的长(结果保留根号).
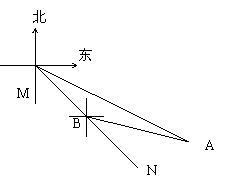
20.(10)金阳新开发区供水工程设计从M到N的一段的路线图如图所示,测得N点位于M点南偏东30º,A点位于M点南偏东60º,以A点为中心,半径为500m的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75º,量得MB=400m,请计算后回答:输水路线是否会穿过文物保护区?
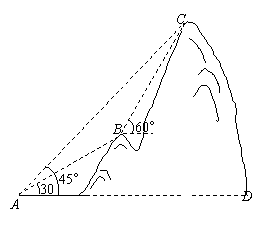 21.(10)如图,某电信部门计划修建一条连结B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200米,电缆BC至少长多少米(精确到0.1米)?
21.(10)如图,某电信部门计划修建一条连结B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B地测得C地的仰角为60°.已知C地比A地高200米,电缆BC至少长多少米(精确到0.1米)?
四、提高题(10)
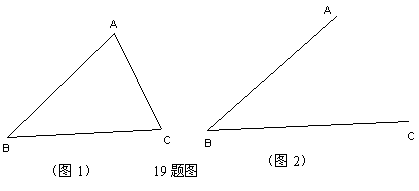
22.(1)如图1,在△ABC 中,∠B 、∠C 均为锐角,其对边分别为b、c,
求证:![]() =
=![]() ;
;
(2)在△ABC 中,AB=![]() ,AC=
,AC=![]() ,∠B =450,问满足这样的△ABC 有几个?在图2中作出来(不写作法,不述理由)并利用(1)的结论求出∠ACB的大小。
,∠B =450,问满足这样的△ABC 有几个?在图2中作出来(不写作法,不述理由)并利用(1)的结论求出∠ACB的大小。