分式运算有技巧
山东省郓城县随官屯中学 周长诗
一、【顺次相加法】
【例1】计算:![]()
【分析】本题中有四个分式相加减,如果采用直接通分化成同分母的分式相加减,公分母比较复杂,其运算难度较大.不过我们注意到若把前两个分式相加,其结果却是非常简单的.因此我们可以采用逐项相加的办法.
【解】![]() =
=![]()
=![]()
=![]()
【例2】计算:![]()
【分析】本题的解法与例1完全一样.
【解】![]() =
=![]()
=![]()
=![]()
二、【整体通分法】
【例3】计算:![]()
【分析】本题是一个分式与整式的加减运算.如能把(-a-1)看作一个整体,并提取“-”后在通分会使运算更加简便.通常我们把整式看作分母是1的分式.
【解】![]() =
=![]() =
=![]() .
.
【例4】计算:![]()
【解】![]()
=![]()
三、【分组运算法】
【例5】计算:![]()
【分析】本题项数较多,分母不相同.因此,在进行加减时,可考虑分组.分组的原则是使各组运算后的结果能出现分子为常数、相同或倍数关系,这样才能使运算简便.
【解】![]()
=![]()
=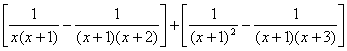
=![]()
=![]()
=![]()
四、【巧用拆项法】
【例6】计算:![]() .
.
【分析】本题的10个分式相加,无法通分,而式子的特点是:每个分式的分母都是两个连续整数的积(若a是整数),联想到![]() ,这样可抵消一些项.
,这样可抵消一些项.
【解】原式=![]()
=![]()
=![]() =
=![]()
四、【分式化简法】
【例5】计算:![]()
【分析】本题若采用直接通分的话,运算量较大,因此我们可采用把分式先化简的方法.在这里有![]() ,
,![]() =
=
![]() .
.
【解】原式=![]()
=![]()
=![]()
=![]()
=![]()