函数及其图象检测

（时间90分钟，满分100分）

一、选择题（3′×10=30′）

1、一次函数y=2x－3的图象一定经过（　　）象限

A、第一　　 B、第二　　　C、第三　　　　　 D、第四

2、如图点P是反比例函数y=上一点，　　　　　　　 y

过点P作y轴的垂线，若构成的三角形面积是6，　　 o

则该反比例函数解析式是（　）　　　　　　　　　　　

A、y=－　　　 B、y=　　　　C、y=—　　　　D、y=

3、购买单价是0.4元的铅笔，总金额y(元)与铅笔X（支）之间的函数关系式，用图象表示正确的是（　　）

　　　　　　 y　　　　　　　　　　　　　　　 y

　　　　　　　　　 x　　　　　　　　　　　　　　　　 x　　　

　　　　　 A　　　　　　　　　　　　　　　　 B

　　　　　　 y　　　　　　　　　　　　　　　　 y

　　　　　　　　　 x　　　　　　　　　　　　　　　　 x

•

　　　　　 C　　　　　　　　　　　　　　　　　 D

4、过两点A（3，4），B（－2，4）作直线AB则AB（　）

A、平行于x轴　　　　　　 B、平行于y轴

C、经过原点　　　　　　　　　　　 D、无法确定

5、关于函数y=－3x+6，下列说法正确的是（　）

A、图象必过点（－3.2）　　 B、图象经过第一、二、三象限

C、当x＞2时，y＜0　　　　　 D、y随x的增大而增大

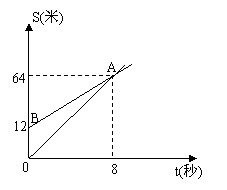6、如图，OA，BA分别表示甲乙两名学

生运动的一次函数图示，根据图象判断快　　　　　　　

者速度每秒比慢者快（　）

A、2.5m　　　　　　　B、2m　　　　　　

C、1.5m　　　　　　　 D、1m　　　　　　　　　　　　　

7、市内电话的收费标准为：3分钟以内（含3分钟）收费0.22元，超过3分钟，每增加1分钟（不足1分钟按1分钟计算）加收0.11元，那么当时间超过3分钟时，电话费y（元）与时间t（分）之间的函数关系式为（　）

A、y=0.11t(t＞3,t为整数)　　　B、y=0.11t+0.22(t＞3,t为整数)

C、y=0.11t－0.22(t＞3,t为整数)　D、y=0.11t(t－3)+0.22(t＞3,t为整数)

8、函数y=与y=bx+a在同一坐标系内的图象可能是（　）

o　　　 x　　　　 o　　　 x　　 o　　 x　　　 o　　 x

A　　　　　　　 B　　　　　　　 C　　　　　　 D

9、已知直线y=kx+b(k≠o) 与x轴交点在x轴的正半轴，下列结论1、k＞o,b＞o 2、k＞o,b＜o　 3、k＜o,b＞o　4、k＜o, b＜o,其中正确的个数是（　　）

A、1个　　　　 B、2个　　　　　 C、3个　　　D、4个

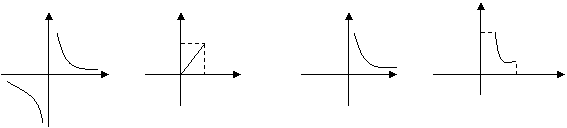
10、面积为2的△ABC，一边长为x，这边上的高为y，则y与x的变化规律用图象表示大致是（　　）

y　　　　　　 y　　　　　　　　 y　　　　　　　 y

　　　　　　　 2 　　　　　　　　　　　　　　　4

　　　　 x　　　　　 2 x　　　　 o　　 x　　　　　 4　x

A　　　　　 B　　　　　　　　 C　　　　　　 D

二、填空（3′×8=24′）

11、若直线y=－3x+5的图象与y=kx+b,平行则k=______b_=___

12、写出一个经过点（－5，3）的一次函数解析式　　　　　

13、在直角坐标系内有两点A（－1，2），B（1，4）在x轴上取一点P，使△ABP的周长最小，则P点坐标是　　　　

14、点P（－2，5）到y轴的距离是　　　　　

15、函数y=中自变量x的取值范围是　　

16、若点m（a－1,b－1）在第一象限，则点N（1－a,1－b）关于x轴的对称点P在第　　　象限。

17、直线y=x+2上有两点A（1，a），B（－2，b）有a_____b

18、对于反比例函数y=与一次函数y=x+3，请说出它们的两个相同点，（1）、　　　　　　，（2）、　　　　　　；再说出它们的两个不同点（1）、　　　　　　，（2）、　　　　　　　　。

三、解答题（19—22#，每题7′，23#，24#10′）

19、已知y=y₁+y₂，其中y₁与x成正比，y₂与x成反比。当x=1时，y=7，当x=3时，y=13，求当x=－1时y的值。

20、已知一直线经过P（0，－2）且与坐标轴围成的三角形面积为3，求该直线解析式。

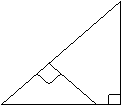
21、如图，△ABC中，∠C=90⁰，P为AB上一动点，且点P不与点A重合，过点P作PE⊥AB交AC边于点E，若AB=10，AC=8，设PE的长为X，四边形PECB的周长为y,求y与x之间的函数关系式。

A　　　　　 E　　 C

22、阅读下面材料，再回答问题：

一般地，如果函数y=f(x)对于自变量取值范围内的任意x,都有f（- x）=－f(x)就叫做奇函数;如果函数y= f (x)对于自变量取值范围内的任意x,都有f(－x)=f(x),那么y=f(x)就叫做偶函数。

例如:f(x)=x³+x

当x取任意实数时,f(－x)=(－x)³+(－x)=－x³－x=－(x³+x)

即f(－x)=－f(x)

所以f(x)=x³+x为奇函数

又如f(x)=x

当x取任意实数时，f(－x)=－x=x=f(x)

即f(－x)=f(x)

所以f(x)=x是偶函数

问题（1）：下列函数中

①y=x⁴②y=x²+1　　　 ③ y=　　　 ④y=x+

所有奇函数是　　　，所有偶函数是　　　（只填序号）。

问题（2）：请你再分别写出一个奇函数、一个偶函数。

23、某果品公司欲请汽车运输公司或火车货运站，将60吨水果从A地运到B地。已知汽车和火车从A地到B地的运输路程均为5km，这两家运输单位在运输过程中，除都要收取运输途中每吨每小时5元的冷藏费外，要收取的其他费用及有关运输资料如下表：

运输工具

行驶速度

（KM/h）

运费单价

（天/吨·千米）

装卸总费用

（元）

汽车

3000

火车

1.7

4620

(1)　请分别表示出这两家运输单位运送这批水果所要收取的总费用y₁(元)和y₂(元)(用含s的式子表示)

(2)　为减少费用,你认为果品公司应该选择哪家运输单位运送更为合算?

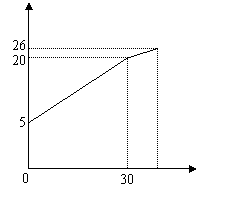
24、一农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售。售出土豆千克数与他手中持有的钱数（含备用钱）的关系如图所示，结合图象回答下列问题：

（1）农民自带的零钱是多少？

（2）降价前，他每千克土豆出售的价格是多少？

函数及其图象检测

A B C D

A　　　　　　　 B　　　　　　　 C　　　　　　 D