解直角 三角形测试题
一. 选择题：（每小题2分，共20分）
1. 在△EFG中，∠G=90°，EG=6，EF=10，则cotE=（ ）
A.
B. 
C. 
D. 
2. 在△ABC中，∠A=105°，∠B=45°，tanC的值是（ ）
A. 
B. 
C.
1 D. 
3. 在△ABC中，若
，
，则这个三角形一定是（ ）
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
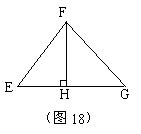
4. 如图18，在△EFG中，∠EFG=90°，FH⊥EG，下面等式中，错误的是（ ）
A.
B. 
C. 
D. 
5. sin65°与cos26°之间的关系为（ ）
A. sin65°<cos26° B. sin65°>cos26°
C. sin65°=cos26° D. sin65°+cos26°=1
6. 已知30°<α<60°，下列各式正确的是（ ）
A. 
B.
C. 
D.
7. 在△ABC中，∠C=90°，
，则sinB的值是（ ）
A. 
B. 
C. 
D. 
8. 若平行四边形相邻两边的长分别为10和15，它们的夹角为60°，则平行四边形的面积是（ ）米2
A.
150 B. 
C. 9 D. 7
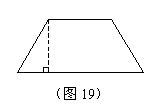
9. 如图19，铁路路基横断面为一个等腰梯形，若腰的坡度为i=
2∶3，顶宽是3米，路基高是4米，则路基的下底宽是（ ）
A. 7米 B. 9米 C. 12米 D. 15米
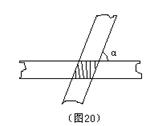10. 如图20，两条宽度都为1的纸条，交叉重叠放在一起，且它们的交角为α，则它们重叠部分（图中阻影部分）的面积为（ ）
A. 
B. 
C. 
D. 1
二. 填空题：（每小题2分，共10分）
11. 已知0°<α<90°，当α=__________时，
，当α=__________时，
。
12. 若
，则锐角α=__________。
13. 在Rt△ABC中，∠C=90°，
，
，则a=__________，b=__________，c=__________，cotA=__________。
14. 若一个等腰三角形的两边长分别为2cm和6cm，则底边上的高为__________cm，底角的余弦值为__________。
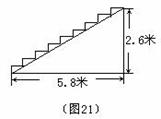
15. 酒店在装修时，在大厅的主楼梯上铺设某种红色地毯，已知这种地毯每平方米售价30元，主楼梯宽2米，其侧面如图21所示，则购买地毯至少需要__________元。
三. 解答题：（16、17每小题5分，其余每小题6分共70分）
16. 计算
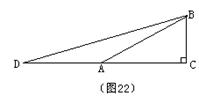
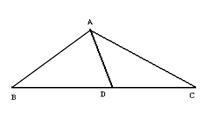
17. 如图22，在△ABC中，∠C=90°，∠BAC=30°，AD=AB，求tanD。
18. 已知直角三角形中两条直角边的差是7cm，斜边的长是13cm，求较小锐角α的各三角函数值。
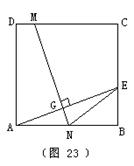
19. 如图23，ABCD为正方形，E为BC上一点，将正方形折叠，使A点与E点重合，折痕为MN，若
。
（1）求△ANE的面积；（2）求sin∠ENB的值。
20. 已知在△ABC中，
，AC=2，BC边上的高
。 （1）求BC的长；
（2）若有一个正方形的一边在AB上，另外两个顶点分别在AC和BC上，求正方形的面积。
21. 已知，△ABC中，∠BAC=120°，AD平分∠BAC，AB=5，AC=3，求AD的长。
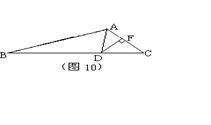
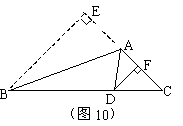
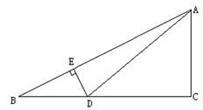22. 如图，在△ABC中，∠C=90°，D是BC边上一点，DE⊥AB于E，∠ADC=45°，若DE∶AE=1∶5，BE=3，求△ABD的面积。
23.已知
中，AD为中线，
，求
的长。
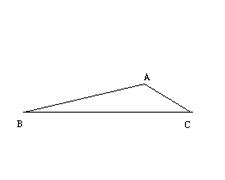
24.在△ABC中，∠A＝1200，AB＝12，AC＝6。求sinB＋sinC的值。
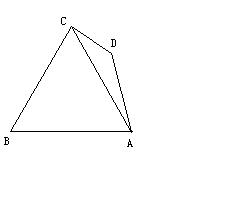25.四边形ABCD中，BC⊥CD，∠BCA＝600，∠CDA＝1350，
。求AD边的长。
26．湖面上有一塔高15米，在塔顶A测得一气球的仰角为40
，又测得气球在水中像的俯角为60，求气球高出水面的高度（精确到0.1米）。
27、由于过度采伐森林和破坏植被，使我国许多地区遭受沙尖暴侵袭。近日A市气象局测得沙尘暴中心在A市正西300公里的B处以10
海里/时的速度向南偏东60的BF方向移动，距沙尘暴中心200公里的范围是受沙尘暴影响的区域。
（1）通过计算说明A市是否受到本次沙尘暴的影响？
（2）若A市受沙尘暴影响，求A市受沙尘暴影响的时间有多长？
试题答案
一. 选择题：
1. A 2. B 3. A 4. C 5. B
6. C 7. D 8. B 9. D 10. A
提示：10. 如图24所示，作AE⊥BC，AF⊥CD，垂足分别为E、F，依题意，有AE=AF=1，可证得∠ABE=∠ADF=α。
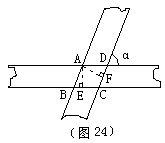
所以可证得△ABE≌△ADF，得AB=AD，
则四边形ABCD是菱形。
在Rt△ADF中，
。
所以
二. 填空题：
11. 30°，30°；12. 60°；13. a=9，b=12，c=15，
；
14. 
15.
504。
提示：13. 设a=3t，c=5t，则b=4t，
由a+b+c=36，得t=3。
所以a=9，b=12，c=15。
。
14. 等腰三角形的腰只能是6，底边为2，腰不能为2，否则不满足三角形两边之和大于第三边，作底边上的高，利用勾股定理求高。
15. 利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为5.8米，2.6米，则地毯的长度为2.6+5.8=8.4米，地毯的面积为8.4×2=16.8平方米，则买地毯至少需要16.8×30=504元。
三. 解答题：
16. 
；
17. 
；
18. 
19. 分析：根据条件可知MN是AE的垂直平分线，则AN=NE。所以∠AEN可以是Rt△EGN的一个锐角，或是Rt△GAN的一个锐角，或是Rt△EBA的一个锐角。
解：∵
∵DC+CE=10，
∴3a+2a=10，∴a=2。
∴BE=2，AB=6，CE=4。
又
。
。
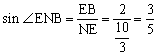20. 根据条件显然有两种情况，如图25。
（1）在图25（1）中，可求CD=1，∠CAD=30°，∠B=30°，∠C=60°，BC=4，所以△ABC是直角三角形。
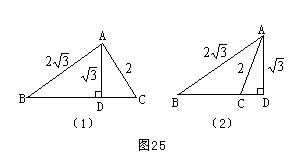
在图25（2）中，可求CD=1，∠CAD=30°，∠B=30°，∠BAD=60°，BC=AC=2，△ABC是等腰三角形，AC平分∠BAD。
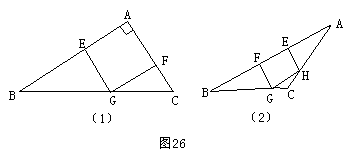（2）在图26（1）中，设正方形边长为x，∵
，解得
。
在图26（2）中，设正方形边长为x。
解得
21. 解法一：过B作CA延长线的垂线，交于E点，
过D作DF⊥AC于F。
∴DF∥BE
∴△FDC∽△EBC
∵AD平分∠BAC
∵∠BAC=120°
∴∠EAB=180°－∠BAC=60°
在Rt△ABE中，
在Rt△ADF中，∵∠DAC=60°
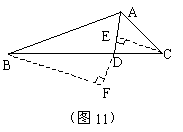
解法二：如图11，过C作CE⊥AD于D，过B作BF⊥AD交AD的延长线于F。
∵AD平分∠BAC，∠BAC=120°
∴∠BAD=∠CAD=60°。
在Rt△AEC中，
在Rt△ABF中，
∵CE∥BF
∴△BDF∽△CDE。
∵EF=1
分析：题目中有120°角及它的角平分线，所以有两个60°这个特殊角，要求60°角的一条夹边AD的长，可以构造等边三角形，得到与AD相等的线段。
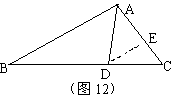解法三：如图12，过点D作DE∥AB交AC于E。
则∠ADE=∠BAD=∠DAC=60°
∴△ADE是等边三角形。
∴AD=DE=AE
设AD=x
∵△ABC∽△EDC
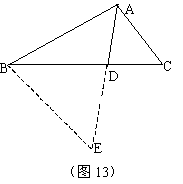解法四：如图13，过B作AC的平行线交AD的延长线于E。
∵AD平分∠BAC，∠BAC=120°
∴∠BAD=∠DAC=∠E=60°。
∴△ADE是等边三角形
∴AE=AB=BE=5
∵AC∥BE
∴△CAD∽△BED
小结：解三角形时，有些图形虽然不是直角三角形，但可以添加适当的辅助线把它们分割成一些直角三角形和矩形，从而可以运用解直角三角形的有关知识去解决这些图形中求边角的问题。另外，在考虑这些组合图形时，要根据题目中的条件和要求来确定边与边，角与角是相加还是相减。
22.解：在△AED中，∵DE⊥AB于E，
又∵DE∶AE=1∶5，∴设DE=x，则AE=5x。
在△ADC中，∵∠C=90°，∠ADC=45°，∴∠DAC=45°，
在Rt△BED和Rt△BCA中，∵∠B是公共角，
∠BED=∠BCA=90°，∴△BED∽△BCA。
∴AB=AE+BE=10+3=13。
23.解：
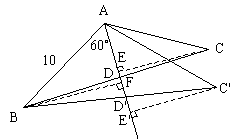
24提示：过C点作CE⊥BA交BA的延长线于E，过点B作BD⊥CA交
CA的延长线于D。
SinB＋sinC＝
25. 提示：作AF⊥AC于F，作AE⊥CD交CD的延长线于E。可求AC＝16，AD＝8
。