平行四边形测试题
（时间：120分钟 满分120分）
一、填空题（每小题3分，共30分）
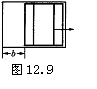
1． (江西省,2003) 如图12.9，一个矩形推拉窗，窗高1.5米，则活动窗扇的通风面积A（平方米）与拉开长度b（米）的关系式是： ．
2． (江西省,2003)用黑白两种颜色的正六边形地面砖按如图12.10所示的规律，拼成若干个图形：
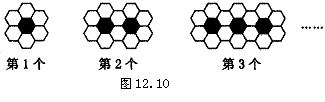
⑴ 第4个图形中有白色地面砖
块；
⑵ 第n个图形中有白色地面砖
块．
3．黑板上画有一个图形，学生甲说它是多边形，学生乙说它是平行四边形，学 生丙说它是菱形，学生丁说它是矩形，老师说这四名同学的答案都正确，则黑板上画的图形是___________________．
4．在正方形ABCD所在的平面内,到正方形三边所在直线距离相等的点有__个．
5．(贵阳市,2002) 四边形ABCD为菱形,∠A=60°, 对角线BD长度为10cm， 则此菱形的周长 cm．
6．已知正方形的一条对角线长为8cm，则其面积是__________cm2．
7．平行四边形ABCD中， AB=6cm，AC+BD=14cm ，则△AOC的周长为_______．
8．在平行四边形ABCD中，∠A=70°，∠D=_________, ∠B=__________．
9．等腰梯形ABCD中，AD∥BC，∠A=120°，两底分别是15cm和49cm，则等腰梯形的腰长为______．
10．用一块面积为450cm2的等腰梯形彩纸做风筝，为了牢固起见，用竹条做梯形的对角线，对角线恰好互相垂直，那么至少需要竹条 cm．
二、选择题（每小题3分，共30分）
11．给出五种图形：①矩形； ②菱形； ③等腰三角形（腰与底边不相等）； ④等边三角形； ⑤平行四边形（不含矩形、菱形）．其中，能用完全重合的含有300角的两块三角板拼成的图形是（ ）
A．②③ B．②③④
C．①③④⑤ D．①②③④⑤
12．(江西省，2003) 如图12.11,设将一张正方形纸片沿右图中虚线剪开后，能拼成下列四个图形，则其中是中心对称图形的是（ ）
 |
13．四边形ABCD中，∠A︰∠B︰∠C︰∠D=2︰2︰1︰3，则这个四边形是（ ）
A．梯形 B．等腰梯形
C．直角梯形 D．任意四边形
14．要从一张长40cm，宽20cm的矩形纸片中剪出长为18cm，宽为12cm的矩形纸片则最多能剪出（ ）
A．1张 B．2张
C．3张 D．4张
15． (北京市，2002) 如图12.12，在平行四边形ABCD中，CE是∠DCB的平分线，F是AB的中点，AB＝6，BC＝4，则AE︰EF︰FB为（ ）
A．1︰2︰3 B． 2︰1︰3
C． 3︰2︰1 D． 3︰1︰2
16．（福建省，2002）下列说法中错误的是（ ）
A．两条对角线互相平分的四边形是平行四边形；
B．两条对角线相等的四边形是矩形；
C．两条对角线互相垂直的矩形是正方形；
D．两条对角线相等的菱形是正方形．
17．下列说法正确的是（ ）
A．任何一个具有对称中心的四边形一定是正方形或矩形；
B．角既是轴对称图形又是中心对称图形；
C．线段、圆、矩形、菱形、正方形都是中心对称图形；
D．正三角形、矩形、菱形、正方形是轴对称图形，且对称轴都有四条．
18．（山西省，2002）点A、B、C、D在同一平面内，从①AB//CD；②AB＝CD；③BC//AD；④BC＝AD四个条件中任意选两个，能使四边形ABCD是平行四边形的选法有（ ）
A．①② B．②③
C． ①③ D． ③④
19．(江西省,2002) 已知ABCD是平行四边形，下列结论中不一定正确的是( )
A．AB=CD B．AC=BD
C．当AC⊥BD时，它是菱形 D．当∠ABC=90°时，它是矩形
20．平行四边形的两邻边分别为6和8，那么其对角线应（ ）
A．大于2， B．小于14
C．大于2且小于14 D．大于2或小于12
三、解答题（第21～26每题8分，第27题12分，共60分）
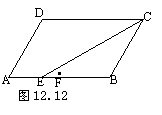
21．（新疆，2002）如图12.13，已知四边形ABCD是等腰梯形， CD//BA,四边形AEBC是平行四边形．请说明：∠ABD＝∠ABE．
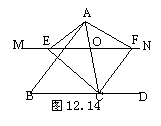
22．如图12.14，在△ABC中，点O是AC边上的一动点， 过点O作直线MN//BC, 设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．
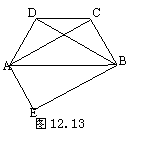（1）说明EO＝FO；
（2）当点O运动到何处时，四边形AECF是矩形？
并说明你的结论．
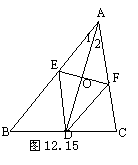23．如图12.15，AD是△ABC的角平分线，DE∥AC交AB于
点E，DF∥AB交AC于F． 试确定AD与EF的位置关系，
并说明理由．
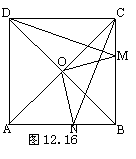
24．如图12.16，在正方形ABCD的边BC上任取一点M，过点C作CN⊥DM交AB于N，设正方形对角线交点为O，
试确定OM与ON之间的关系，并说明理由．
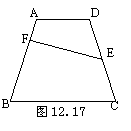
25．如图12.17，等腰梯形ABCD中，E为CD的中点，
EF⊥AB于F，如果AB=6，EF=5，求梯形ABCD的面积．
26． (江西省，2003) 如图12.18,有一长方形餐厅，长10米，宽7米，现只摆放两套同样大小的圆桌和椅子，一套圆桌和椅子占据的地面部分可看成半径为1.5米的圆形（如左下图所示）．在保证通道最狭窄处的宽度不小于0.5米的前提下，此餐厅内能否摆下三套或四套同样大小的圆桌和椅子呢？请在摆放三套或四套的两种方案中选取一种，在右下方 14×20方格纸内画出设计示意图．（提示：①画出的圆应符合比例要求； ②为了保证示意图的清晰，请你在有把握后才将设计方案正式画在方格纸上．说明：正确地画出了符合要求的三个圆得5分，正确地画出了符合要求的四个圆得8分．）
 |
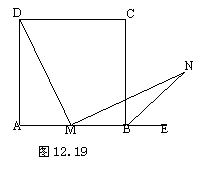27．如图12.19, 在正方形ABCD中, M为AB的中点，
MN⊥MD，BN平分∠CBE并交MN于N．
试说明：MD=MN．
1．A=
b (点拨：利用矩形的面积等于长与宽的积．)
2．（1）18；（2）4n+2（点拨：每相邻两个大正六边形有两块白色地砖是公共的，因此第n个图形中有白色地面砖4n+2块．）
3．正方形（点拨：既是矩形又是菱形的四边形是正方形．）
4．5个点（点拨：正方形的中心O；正方形四个外角角平分线的交点．）
5．40（点拨：当∠A=60°时，菱形的边长等于它较短的对角线长．）
6．32（点拨：正方形的两条对角线把正方形分成四个全等的小等腰直角三角形．）
7．13㎝(点拨：平行四边形的对角线互相平分，则OA+OB=7㎝．)
8．110°,110°（点拨：平行四边形的对角相等，邻角互补．）
9．34㎝（点拨：过点A作腰的平行线得到等边三角形，则腰长等于两底的差．）
10．60（点拨：设对角线长为a，过上底的一个端点作对角线的平行线，与下底及梯形的另一条腰构成等腰直角三角形，则它的面积=
a2=450，a=30．）
11．C(点拨：当两块三角板的最小边重合时，可得到平行四边形或腰和底边不相等的等腰三角形；当它们的斜边重合在一起时，可得到矩形．)
12．C（点拨：图（B）绕小正方形的中心旋转180°，能与原来的图形重合．）
13．C（点拨：四边形的四个内角分别为90°、90°、45°、135°．）
14．C（点拨：在矩形的长上依次剪三个12㎝，再在宽上剪18㎝．）
15．B（点拨：BE=BC=4，AE=2，BF=3，则EF=BE－BF=1．）
16．B（点拨：对角线相等的平行四边形是矩形．）
17．C（点拨：菱形也是中心对称图形，A错；角不是中心对称图形，B错．）
18．B（点拨：由①②，①③，③④，②④的组合都能得到平行四边形．）
19．B（点拨：平行四边形ABCD不一定是矩形，因而它的对角线不一定相等．）
20．C（点拨：利用三角形两边之和大于第三边，两边之差小于第三边．）
21．AD=BC=AE，BD=AC=BE，AB=AB，则△AEB≌△ADB，故∠ABD=∠ABE．
22．(1) CE平分∠ACB，则∠ACE=∠BCE，而MN//BC，得到∠OEC=∠BCE，所以∠ACE=∠OEC，从而EO=OC，同理OC=OF，故EO=FO；（2）当点O运动到AC的中点处时，四边形AECF是矩形．先得到∠ECF=90°，再根据有一个角是直角的平行四边形是矩形进行识别．
23．AD⊥EF．根据有一组邻边相等的平行四边形
是菱形，确定四边形AEDF是菱形，所以AD⊥EF．
24．OM⊥ON，OM=ON．先说明△DCM≌△CBN
得CM=BN，再推出△OCM≌△OBN得OM=ON．
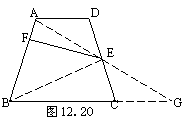
25．如图12.20，连结AE交BC的延长线于G点，连结BE．先说明△ADE≌△GCE，得到AE=GE， S△ABG=S梯形ABCD=2S△ABE=2×15=30．
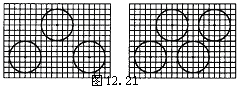26．摆放三套或四套的设计方案如图12.21
所示．关键是确定这些圆的圆心位置（圆
心分别在等腰三角形和平行四边形的顶点
处），另外，设计的示意图要符合比例要求：
（1）每个圆的半径为1.5㎝；（2）每个圆的圆心到方格纸外边框的距离不小于2㎝；（3）设计两圆的圆心的距离不小于3.5㎝．
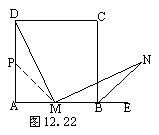27．如图12.22，将△BMN以∠DMN的角平分线
为轴翻折至△PDM的位置，即取AD的中点P，
连结PM．从而△MPD≌△NBM，故DM=MN．