§19.1平行四边形练习题
一、耐心填一填!
1、![]() ABCD中,∠B-∠A=40°,则∠D=__。
ABCD中,∠B-∠A=40°,则∠D=__。
2、![]() ABCD的周长是44cm,AB比AD大2cm,则AB=__cm,AD=__cm。
ABCD的周长是44cm,AB比AD大2cm,则AB=__cm,AD=__cm。
3、平行四边形的两个相邻内角的平分线相交所成的角的度数是__。
 4、平行四边形的两条邻边的比为2∶1,周长为60cm,则这个四边形较短的边长为__。
4、平行四边形的两条邻边的比为2∶1,周长为60cm,则这个四边形较短的边长为__。
5、如图所示,在![]() ABCD中,AE⊥BC于E,AF⊥CD于F,
ABCD中,AE⊥BC于E,AF⊥CD于F,
∠BAD=120°,BE=2,FD=3,则∠EAF=___,![]() ABCD的周长为__。
ABCD的周长为__。
6.若平行四边形的两邻边的长分别为16和20,两长边间的距离为8,
则两短边间的距离为_____________.
7、![]() ABCD
,AB=6cm,BC=8cm,∠B=70°,则AD=________,CD=______,
ABCD
,AB=6cm,BC=8cm,∠B=70°,则AD=________,CD=______,
∠D=__________,∠A=_________,∠C=__________.
 8、平行四边形周长为50cm,两邻边之差为5cm,各边长为
。
8、平行四边形周长为50cm,两邻边之差为5cm,各边长为
。
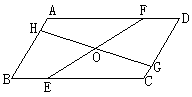
9.如图,平行四边形ABCD的周长为30cm,它的对角线AC和BD相交于O,且△AOB的周长比△BOC的周长大5cm,AB= 、BC= 。
10.平行四边形ABCD的对角线AC和BD相交于O,则其中全等的三角形有___对。
二、精心选一选!
11、下面各条件中,能判定四边形是平行四边形的是 ( )
A、对角线互相垂直 B、对角线互相平分 C、一组对角相等 D、一组对边相等
12、已知下列四个命题:①一组对边平行且相等的四边形;②两组对角分别相等的四边形;③对角线相等的四边形;④对角线互相平分的四边形。其中能判定平行四边形的命题的个数为 ( )
A、1个 B、2个 C、3个 D、4个
13、平行四边形的两条对角线及一边的长可依次取 ( )
A、6、6、6 B、6、4、3 C、6、4、6 D、3、4、5
14、以不共线三点为三个顶点作平行四边形,一共可作平行四边形的个数是 ( ) A、2个 B、3个 C、4个 D、5个
15、四边形ABCD的四个角∠A∶∠B∶∠C∶∠D满足下列哪一条件时,四边形ABCD是平行四边形?( )
A、1∶2∶2∶1 B、2∶1∶1∶1 C、1∶2∶3∶4 D、2∶1∶2∶1
 16、如图所示,在
16、如图所示,在![]() ABCD中,EF过对角线的交点,若AB=4,BC=7,OE=3,则四边形EFDC的周长是( )
ABCD中,EF过对角线的交点,若AB=4,BC=7,OE=3,则四边形EFDC的周长是( )
A、14 B、11 C、10 D、17
17、四边形ABCD中,AD∥BC,要判定四边形ABCD是平行四边形,
还应满足( ) A、∠A+∠C=180° B、∠B+∠D=180°
C、∠A+∠B=180° D、∠A+∠D=180°
18、根据下列条件,得不到平行四边形的是( )
A、 AB=CD,AD=BC B、AB∥CD,AB=CD
C、AB=CD,AD∥BC D、AB∥CD,AD∥BC
19、若![]() ABCD的周长为40cm,ΔABC的周长为27cm,则AC的长是( )
ABCD的周长为40cm,ΔABC的周长为27cm,则AC的长是( )
A、13cm B、3cm C、7cm D、11.5cm
20、平行四边形的对角线长分别是x和y,一边长为12,则下列各组数据可能是x与y的值的是( )
A、 8与14 B、10与14 C、18与20 D、10与36
21、![]()
![]() 中
中![]() ,则
,则![]() 和
和![]() 的度数分别为( )
的度数分别为( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
三、说理与简答
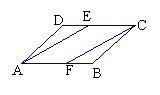 22、在
22、在![]() ABCD中,E、F分别在DC、AB上,且DE=BF。
ABCD中,E、F分别在DC、AB上,且DE=BF。
求证:四边形AFCE是平行四边形。
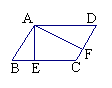
 23、如图所示,四边形ABCD是平行四边形,且∠EAD=∠BAF。
23、如图所示,四边形ABCD是平行四边形,且∠EAD=∠BAF。
① 求证:ΔCEF是等腰三角形;
②观察图形,ΔCEF的哪两边之和恰好等于![]() ABCD的周长?并说明理由。
ABCD的周长?并说明理由。
 24、如图所示,
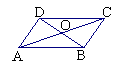
24、如图所示,![]() ABCD中的对角线AC、BD相交于O,EF经过点O与AD延长线交于E,与CB延长线交于F。 求证:OE=OF
ABCD中的对角线AC、BD相交于O,EF经过点O与AD延长线交于E,与CB延长线交于F。 求证:OE=OF
 25、如图所示,在ΔABC中,AE平分∠BAC交BC于E,DE∥AC交AB于D,
25、如图所示,在ΔABC中,AE平分∠BAC交BC于E,DE∥AC交AB于D,
过D作DF∥BC交AC于F。 求证: AD=FC
|
(1)
求证:DF=BG; (2)求![]() 的度数.
的度数.
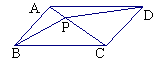
27、如图所示,在![]() ABCD中,P是AC上任意一点,求证:
ABCD中,P是AC上任意一点,求证:![]()
 28、如图所示,
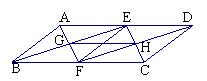
28、如图所示,![]() ABCD中,E、F分别为AD、BC的中点,AF与BE相交于G,DF与CE相交于H,连结EF、GH。 求证:EF、GH互相平分。
ABCD中,E、F分别为AD、BC的中点,AF与BE相交于G,DF与CE相交于H,连结EF、GH。 求证:EF、GH互相平分。
29、如图,在□ABCD中,E、F、G、H分别是四条边上的点,且满足BE=DF,CG=AH,连接EF、GH。求证:EF与GH互相平分。