图形的相似
（90分钟完卷，满分100分）
一、选择题（每小题3分，共30分）
1、下列说法正确的是（ ）
A．两个等腰三角形一定相似 B．两个菱形一定相似
C．两个梯形一定相似 D．两个正方形一定相似
2、在比例尺为1：的地图中，量得甲、乙两地的距离是25cm，则两地的实际距离为（ ）
A．53×166m B．1.25×166m C．1.25×166km D．cm
3、已知△ABC的三边长分别为5，12，13，和△ABC相似的△A1B1C1的最大边长为26，则△A1B1C1的周长是（ ）
A．50 B．40 C．60 D．30
4、如果一个4米高的旗杆的影长为6米，同它临近的一个建筑物的影长是24米，那么这个建筑物的高度是（ ）米。
A．16米 B．17米 C．18米 D．20米
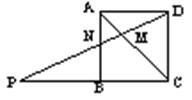
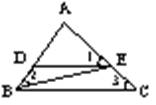5、如图，若∠1=∠2=∠3，则图中的相似三角
形有（ ）。
A．2对 B．3对
C．4对 D．5对
6、两个相似多边形的一组对应边分别为5cm和7.5cm，如果它们的面积之和为130cm2，则较小的多边形的面积是（ ）。
A．50cm2 B．40 cm2 C．30 cm2 D．45 cm2
7、在△ABC中，∠C=90°CD是高，则下列式子中，正确的是（ ）。
A．AC2=AD·BC B．AC2=BD·AB
C．AC2=AD·AB D．AC2=BD·BC
8、张明同学想利用树影测量校园内的树高，他在某一时刻测得小树高为1.5米时，其影长为1.2米，当他测量教楼旁的一棵大树影长时，因大树靠近教楼，有一部分影子在墙上，经测量，地面部分影长为6.4米，墙上影长为1.4米，那么这棵大树高约（ ）米。
A．9.1 B．9.2 C．9.4 D．9.5
9、将△ABC的三个顶点的横坐标都乘以-1，纵坐标不变，则所得图形与原图形的关系是（ ）。
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．不存在对称关系
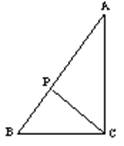
10、如图，△ABC中，P为AB上一点，在下列四
个条件中：①∠ACB=∠B，②∠APC=∠ACB
③AC2=AP·AB，④AB·CP=AP·CB
能得出△ABC∽△ACP的是（ ）。
A．①②④ B．①③④ C．②③④ D．①②③
二、填空题（每题4分，共16分）
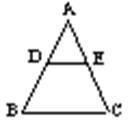11、如图，DE∥BC，
，则
，
若BC=12，则DE= 。
12、如图，有一池塘，要测量两端A、B的
距离，可先在平地上取点C，连接AC并延长到D，
使CD=
，连接DE，如果量得DE的长为36m，
那么池塘的宽AB为 m。
13、如果A、B的坐标分别为A（-4，5），B（-4，2），则将B点向 平移 个单位可得到点A。
14、如图，正方形ABCD中,点N为AB的中点，
连接DN并延长交CB的延长线于点P，连接AC交DN于点M，若PN=3，则DM的长为 。
三、解答题（15—18小题，每小题7分，19—20小题，每小题8分，21小题10分）
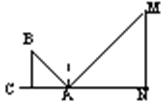
15、如图，为了测量高楼MN的高，在离N点
20m的A处放了一个平面镜，小明沿NA后退到C点，
正好从镜中看到楼顶M点，若AC=1.5m，小明的眼睛
离地面的高度为1.6m，请你帮小明计算一下楼房的高度（精确到0.1m）。
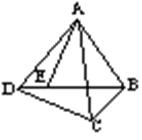
16、如图，点E是四边形ABCD的对角线BD上一点，
且∠BAC=∠BDC=∠DAE，试说明BE·AD=CD·AE。
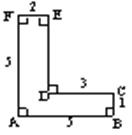17、小明要在电话中告诉同学如图所示的图形，
为了描述清楚，他用什么方法呢？
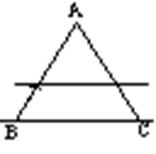18、如图，在△ABC中，AB=7，AC=6，
BC=8，线段BC所在直线以每秒2个单位的速
度沿BA方向运动，并始终保持与原位置平行，
记x秒时，该直线在△ABC内的部分的长度
为y，试写出y关于x的函数关系式，并在直角
坐标系中画出这一函数的图象。
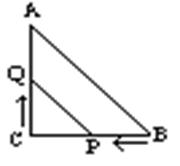19、如图，在△ABC中，∠C=90°，
BC=8cm，AC=6cm，点P从B出发，沿
BC方向以2cm/s的速度移动，点Q从C
出发，沿CA的方向以1cm/s的速度移动，
若P、Q分别从B、C同时出发，经过多长
时间△CPQ与△CBA相似。
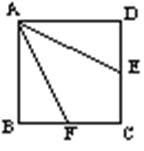
20、在正方形ABCD中，E是DC的中点，
F是BC上一动点，试探索点F在BC上什么位
置时，AE平分∠DAF。
21、如图，等腰梯形ABCD中，AD∥BC，
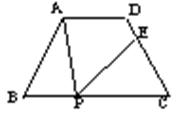AD=3cm，BC=7cm，∠B=60°，P为下底BC上
一点（不与B、C重合），连结AB，过P点作PE
交DC于E，使得∠APE=∠B。
⑴求证：△ABP∽△PCE；
⑵求等腰梯形的腰AB的长；
⑶在底边BC上是否存在一点P，使得DE：EC=5：3？如果存在，求BP的长；如果不存在，请说明理由。