初级中学八年级数学教学质量测试试卷
姓名： ，班级 ，学号
一、 填空题：（每题3分，36分）
1.
16的平方根是______ ，
的立方根是________；
的算术平方根是 。
2.
计算：
。
3. 写出一个图象在第二、四象限的反比例函数的解析式_________。
4. 在实数-2，
，
，0，
，
中，无理数是
。
5. 函数
的自变量x的取值范围是_______________。
6. 已知点A(3，n)关于y轴对称的点的坐标为(-3，2)，那么n的值为 _______ ，点A关于原点对称的点的坐标是 ________。
7. 把直线y＝2x－3向上平移5个单位，得到直线
8.
矩形的长和宽分别是
和
，则矩形的面积是
| x | －2 | －1 | 0 | 1 | 2 | 3 |
| y | 6 | 4 | 2 | 0 | －2 | －4 |
9.
观察分析下列数据，按规律填空：
，2，
，2，
，…，
(第n个数)。
10. 已知一次函数y = ax +b(a，b是常数)，
x与y的部分对应值如下表：
那么方程ax + b = 0的解是___________； 不等式ax + b＞0的解集是____________。
11. 一次函数
的图像经过一、三、四象限，则
的取值范围是
12. 通过平移把点A(2，-3)移到点A′(4，-2)，按同样的平移方式，点B(3，1)移到点B′, 则点B′的坐标是 ________
二、选择题：（每题3分，30分）
13. 化简
的结果是（ ）
A．
B.
C.
D.
14. 下列运算中，错误的是( )
A．
B. 
C. 
D. 
15.
已知
为实数，且
，则
的值为（ ）
A．3 B. – 3 C. 1 D.– 1
16. 下列各点在双曲线y=-
上的是 ( )
A．(
，
)
B. (，
) C. (
，)
D. (，
)
17.
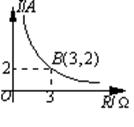某闭合电路中，电源电压为定值，电流I(A)与电阻R(Ω)成反比例，右图表示的是该电路中电流I与电阻R之间函数关系的图象，则用电阻R表示电流I的函数解析式为（ ）
A．
B. 
C. 
D. 
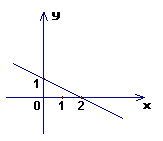
18.
若函数
(
为常数)的图象如图所示，那么当
时，
的取值范围是( )
A．
B. 
C. 
D.
19. 式子
有意义，则点P(a，b)在
( )
A．第一象限 B. 第二象限 C. 第三象限 D. 第四象限
20. 下列各组二次根式中是同类二次根式的是 （ ）
A．
（B） 
（C） 
（D） 
21. 若M 
、N 
、P 
三点都在函数
（
）的图象上，则
的大小关系为（ ）
A．
＞
＞
B. ＞＞ C. ＞＞ D.＞＞
22.
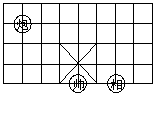如图，是象棋盘的一部分。若
位于点（1，2）上，
位于点（4，－2）上，则
位于点（ ）上。
A．（－1，1） B.（－1，2）
C.（－2，1） D.（－2，2）
三、解答题：（12+8+8+8+8+10）
23. 计算：①
②
－
－
＋
③
④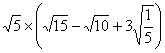
24. 某世界自然保护区，有一种雪白的树蟋蟀，人们发现他15秒钟所叫次数与当地温度之间有近似一次函数关系。下面是蟋蟀所叫次数与温度变化情况对照表：
| 蟋蟀15秒 叫次数x | … | 10 | 19 | 28 | … |
| 温度y（℃） | … | 10 | 15 | 20 | … |
（1）根据表中数据确定:用含x的代数式表示y；
（2）在该地最热的夏天，人们测得这种蟋蟀15秒钟叫了50次，那么该地当时的最高温度大约为多少摄氏度？
25. 若
，且
的算术平方根是3，求
的值。
26. 
求直线
与轴和轴的交点，并画出这条直线及求出这条直线与坐标轴围成三角形的面积。
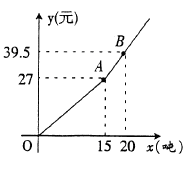
27. 某市选自来水公司为鼓励居民节约用水，采取按月用水量收费办法，若某户居民应交消费(元)与用水量(吨)的函数关系如图所示。分别写出当0≤≤15和≥15时，与的函数关系式；若某用户该月用水21吨，则应交水费多少元？
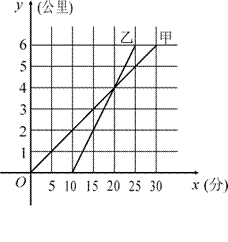
28. 甲骑自行车、乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间的函数关系的图象如右图。 根据图象解决下列问题：
(1) 谁先出发？先出发多少时间？谁先到达终点？先到多少时间？
答： ； ； ； 。
(2) 分别求出甲、乙两人的路程与时间的函数关系式及自变量取值范围？
(3) 在什么时间段内，两人均行驶在途中(不包括起点和终点)？在这一时间段内，请你根据下列情形，分别列出关于行驶时间x的方程或不等式(不化简，也不求解)：
① 甲在乙前面；
②
甲与乙相遇；
③ 甲在乙后面；
姓名： ，班级 ，学号
拓展试题：（选做，4+4+3+10=20分）
1.
已知函数y＝
，则x的取值范围是
。 若x是整数，则此函数的最小值是
。
2. 已知点A（2a+3b,-2）和点B（8，3a+2b）关于x轴对称，那么a+b= 。
3. 有一个装有进、出水管的容器，单位时间内进、出的水量都是一定的。已知容器的容积为600升，又知单开进水管10分钟可把空容器注满，若同时打开进、出水管，20分钟可把满容器的水放完，现已知水池内有水200升，先打开进水管5分钟后，再打开出水管，两管同时开放，直至把容器中的水放完，则能正确反映这一过程中容器的水量Q（升）随时间t（分）变化的图象是（ ）
 |
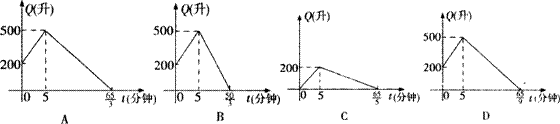4. 一次函数y＝kx＋b（k≠0）的图象经过点（－2，1）和（4，4）
（1）求它的函数关系式，并画出图象；
（2）P为该函数图象上一点，A为该函数图象与x轴的交点，若S
＝6，
求点P的坐标。