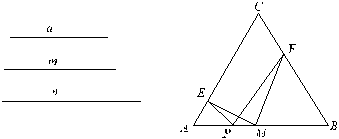初中几何第四章“四边形”测试题
（满分100分，时间90分钟）
一．（每小题2分，共16分）填空题：
（1）
内角和等于它的外角和的多边形的边数
=______。
（2）
矩形的周长是14
，相邻两边的差是1，那么这个矩形的面积是______。
（3）
平行四边形ABCD中，AB=6，BC=12，对边AD和BC的距离是4，则对边AB
和CD间的距离是______。
（4）
面积为
的正方形的对角线长为______。
（5）
矩形的面积为
，一边长是3，那么矩形的对角线长是______。
（6）
菱形两对角线长分别为24和10，则菱形的高为______。
（7）
梯形的下底为17，中位线长11，则梯形的上底长为______。
（8）
菱形两个邻角的比是1：2，周长是24，则菱形的面积为_____。
二．（每小题3分，共24分）选择题：
（1）七边形的对角线的条数是（ ）
（A）10 （B）12 （C）14 （D）16
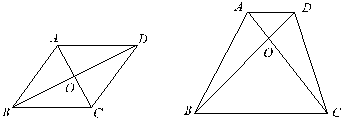
（2）平行四边形ABCD中，对角线AC、BD交于O（如图），则图中全等的三角形的对数为（ ）
|
|
（A）2对 （B）3对 （C）4对 （D）5对
（3）如图，梯形ABCD，AD∥BC，对角线AC、BD交于O，则图中面积相等的三角形有（ ）
（A）4对 （B）3对 （C）2对 （D）1对
（4）不能判定四边形ABCD为平行四边形的题设是（ ）
（A）AB平行且等于CD。
（B）∠A=∠C，∠B=∠D。
（C）AB=AD，BC=CD。
（D）AB=CD，AD=BC。
（5）既是轴对称图形，又是中心对称图形的是（ ）
（A） 等边三角形
（B） 等腰直角三角形
（C） 等腰梯形
（D） 菱形
（6）能判定一个四边形是平行四边形的条件是（ ）
（A） 一组对边平行，另一组对边相等
（B） 一组对边平行，一组对角相等
（C） 一组对边平行，两条对角线相等
（D） 两条对角线垂直且相等
（7）顺次连结四边形四条边的中点，所得的四边形是菱形，则原四边形一定是（ ）
（A） 平行四边形
（B） 对角线相等的四边形
（C） 矩形
（D） 对角线互相垂直的四边形
（8）直角梯形的一个内角为
，较长的腰为6，一底为5，则这个梯形的面积为（ ）
（A）
（B）
（C）25
|
|
（D）或
三．（本题8分）
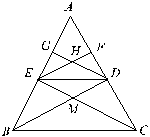
已知：如图，ΔABC中，AB=AC，BD、CE分别平分∠ABC和∠ACB，BD、CE相交于M，EF、DG分别平分∠AED和∠ADE，EF、DE相交于H。
|
|
四．（本题10分）
已知：如图，四边形ABCD中，∠ABC和∠ADC
=
，E、F分别是对角线AC、BD的中点。
求证：EF⊥BD。
五．（本题10分）
 |
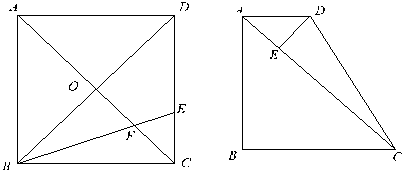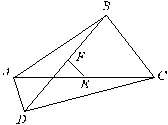
已知：如图，正方形ABCD，对角线AC、BD交于O，BE平分∠DBC交AC于F，交DC于E。
（第5题） （第6题）
求证：
六．（本题10分）
已知：如图，直角梯形ABCD中，AD∥BC，∠B=，AD=2，AB=3，BC=4，DE⊥AC于E。
求：DE长。
七．（本题10分）
已知：线段
、
、（如图）
|
|
求作：平行四边形ABCD，使AB=，对角线AC=，BD=。
（第7题） （第8题）
八．（本题12分）
已知：如图，P是等腰三角形底边AB上一点，PE⊥AC于E，PF⊥BC于F，M是AB的中点。
求证：ME=MF。
初中几何第四章“四边形”测试题
参考答案
一．（1）4
（2） （提示：一组邻边的长分别为3，4）
（3）8 （提示：设对边AB、CD间距离是
，则
）
（4）
（提示：设对角线长，则
）
（5）5 （提示：邻边是4）
（6）
（提示：菱形边长为13）
（7）5
（8）
（提示：菱形的高为
）
二．
| 题号 | （1） | （2） | （3） | （4） | （5） | （6） | （7） | （8） |
| 答案 | C | C | B | C | D | D | B | D |
提示：（8）分类讨论，上、下底都可能是5。
三．提示：∠ADG=∠ACE，∠AEF=∠ABD，ME=MD。
四．提示：连结ED、EB，证明ED=EB。
五．提示：过O作OG∥DE，交BE于G，证OG=OF。
六．
（提示：过D作DF⊥BC于F，可求得DC=
，又可求得AC=5，设AE=
，可得方程
，解得
，再由勾股定理求得DE=
八．提示：连结CM，证ΔMEA≌ΔMFC。