初二数学辅导班练习(1)
一、选择:
1、下列说法正确的是
A.分母等于零,分式有意义 B.分母不等于零,分式有意义
C.分式的值等于零,分式无意义 D.分子等于零,分式的值就等于零
2、若分式
![]() 无意义,则
无意义,则
A. ![]() B.
B. ![]() C.
C. ![]() D.没有这样的有理数
D.没有这样的有理数
3、如果分式![]() 应满足
应满足
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4、分式
![]() 约分,等于
约分,等于
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5、下列分式中最简分式是
A.![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
6、下列各式中正确的是
A.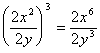 B.
B.![]()
C.![]() D.
D.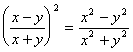
二、填空题:
1、当x= 时,分式![]() 没有意义;
没有意义;
2、已知![]() ;
;
3、在下列各式的括号内填上适当的整数:
(1)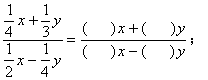 (2)
(2)![]()
5.当![]() 时,分式
时,分式![]() 的值为零.
的值为零.
6.当![]() 时,分式
时,分式![]() 的值为正数
的值为正数
7、计算:![]() ;
;![]() 。
。
三、计算
1、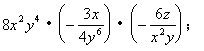 2、
2、![]() ;
;
3、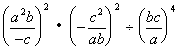 ; 4、
; 4、![]()
四、已知![]() 的值。
的值。
(附加题)
1、请你写一个只含有字母x(数字不限)的分式(要求:(1)x取任何有理数时,分式有意义;(2)此代数式恒为负)___________________。
2、已知x为整数,且![]() 为整数,则所有符合条件的x的值的和是____________。
为整数,则所有符合条件的x的值的和是____________。
3、观察下列各式:
![]() ,
,![]() ;
;![]() ;
;![]() ……想一想,什么样的两数之积等于这两数之和?设n表示正整数,用关于n的等式表示这个规律为______________。
……想一想,什么样的两数之积等于这两数之和?设n表示正整数,用关于n的等式表示这个规律为______________。
4、已知x+![]() ,则x2+
,则x2+![]() 的值是____________________。
的值是____________________。
5、已知ax=3,则![]() 的值是_____________________。
的值是_____________________。
6、已知![]() 有意义,则x的取值范围是_________________。
有意义,则x的取值范围是_________________。
7、(1)观察下列各式:
![]() ;
;![]() ;
;![]() ;
;![]() ……
……
由此可推断![]() =____________________。
=____________________。
( 2)请猜想能表示(1)的特点的一般规律,用含字m的等式表示出来,并证明(m表示整数)
(3)请用(2)中的规律计算
![]()
8、请先阅读下列一段文字,然后解答问题:
初中数学课本中有这样一段叙述:“要比较a与b的大小,可以先求出a与b的差,再看这个差是正数、负数还是零,”由此可见,要判断两个代数式值的大小,只要考虑它们的差就可以。
问题:甲、乙两人两次同时在同一粮店购买粮食(假设两次购买粮食的单价不相同)甲每次购买粮食100kg,乙每次购粮用去100元。
(1)设第一、第二次购粮单价分别为x元/kg和y元/kg,用含x、y的代数式表示:甲两次购买粮食共需付粮款______________元,乙两次共购买____________kg粮食。叵甲两次购粮的平均单价为每千克Q1元,乙两次购粮的平均单价和每千克Q2元,则Q1=_________,Q2=___________。
(2)若规定:谁两次购粮的平均单价低,谁的购粮方式就更合算,请你判断甲、乙两人的购粮方式哪一个更合算,并说明理由。
9、若方程![]() 的解是正数,求a的取值范围。
的解是正数,求a的取值范围。
对这道题,有位同学作了如下解答:
解:去分母得:2x+a=-x+2
化简得:3x=2-a
∴ x=![]()
欲使方程的根为正数,必须![]() >0
>0
解得a<2
∴ 当a<2时,方程![]() 的是正数。
的是正数。
上述解法是否有误,若有错误请指出错误的原因,并写出正确解法,若无错误,说明第一步解决的依据。
10、阅读下列材料:
∵ ![]()
![]() )
)
![]() )
) ![]()
……
∴ ![]()
=![]() )
)
解答下列问题:
(1)在和式![]() 中,第5项为____________,第n项为___________,上述求和的想法是:通过运用_______________法则,将和式中的各分数转化为两个数之差,使得首末两面外的中间各项可以____________,从而达到求和目的。
中,第5项为____________,第n项为___________,上述求和的想法是:通过运用_______________法则,将和式中的各分数转化为两个数之差,使得首末两面外的中间各项可以____________,从而达到求和目的。
(2)利用上述结论计算
![]()