初二数学练习⑹ 课作 班级 姓名
1.如图,若∠ADE= 或∠C=
时,△ADE∽△ABC;若
时,
△ADE∽△ABC,理由是 .
2.下列条件中,判断△ABC与△A´B´C´是否相似？并说明理由.
⑴∠C=∠C´=90°,∠B=∠B´=50°.( )理由 .
⑵AB=AC,A´B´=A´C´,∠B=∠B´. ( )理由 .
⑶∠B=∠B´,
. (
)理由 .
⑷∠A=∠A´,
. (
)理由 .
3.△ABC中，∠A=47°，AB=1.5cm，AC=2cm；△DEF中，∠E=47°，ED=2.8cm，EF=2.1cm，则△ ∽△ .
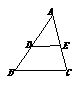
4.如图，要使△AEF∽△ACB，已具备的条件是 ，还需补充的条件是
或 或 .
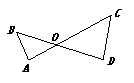
5. 如图，线段AC、BD相交于点O，要使△AOB∽△DOC，已具备的条件是 ，还需补充的条件是 或 或 .
6.如图，△ABC中CD为高线，AD=4,CD=3,则当DB= 时，△ADC∽△CDB.
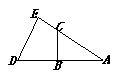
7.如图,B、C在△ADE的边AD、AE上，且AC=6,AB=5,EC=4,DB=7,则BC:DE= .
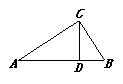
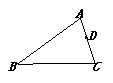8.如图，在△ABC中，AB=15,AC=8,在AC上取一点D,使AD＝3，则在AB上取点E,使△ADE和△ABC相似，则AE长为 .
|
|  | |||||||
| |||||||||
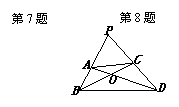
9.如图,AD、BC交于点O,BA、DC的延长线交于点P,PA·PB=PC·PD.
试说明：①△PAC∽△PDB;②△PBC∽△PDA;③△AOB∽△COD.
 |
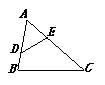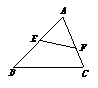
10.如图，D、E分别为AB、AC边上两点，且AD=5,BD=3,AE=4,CE=6.
试说明：①△ADE∽△ACB;②∠ADE=∠C.
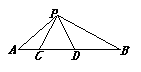11.如图,点C、D在线段AB上，△PCD是等边三角形.
①当AC、CD、DB满足怎样的关系时△ACP∽△PDB;
②当△ACP∽△PDB时，求∠APB.
初二数学练习⑹ 家作 班级 姓名
1.下列条件中,能识别△ABC与△A´B´C´相似的有 ( )
①∠A＝45°,∠B=80°,∠A´＝45°,∠C´=55°; ②∠A=∠A´=45°,∠B=75°,∠B´=50°;③∠A=47°,AB=1.5,AC=2, ∠A´=47°,A´B´=2.8, B´C´=2.1;④∠A=35°,AB=24,AC=30, ∠A´=35°,A´B´=32, A´C´=40 . A.1个 B.2个 C.3个 D.4个
2．下列说法中，正确的是 ( ) A. 有一个角是90°的两个等腰三角形相似
B. 有一个角是45°的两个等腰三角形相似 C. 放大镜下的图形与原图形不一定相似
D. 有一个角对应相等且有两条边对应成比例的两个三角形相似
3．D为△ABC边AB上一点，下列说法中错误的是 ( )
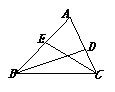A.若∠ACD=∠B,则△ACD∽△ABC
B.若∠ADC=∠ACB,则△ACD∽△ABC
C.若AC2=AD·AB,△ACD∽△ABC D.若AC:CD=AB:BC, △ACD∽△ABC
4.如图,在△ABC中,点D、E在AC、AB边上，要得到△ABD∽△ACE,已经
具备了条件 ，还需要添加的条件是 或 或 .
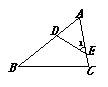5.如图，直线DE交△ABC的两边AB、AC于点D、E,且
,
试说明：∠1＝∠B.
 |
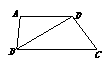6.如图,在梯形ABCD中,AD∥BC,BD2=AD·BC,试说明△ADB∽△DBC.
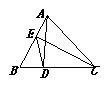7.在△ABC中，AD⊥BC,垂足为D,EC⊥AB,垂足为E,试说明△BDE∽△BAC.
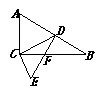8.如图，△ABC中，∠ACB=90°,D为AB上一点，CE⊥CD,且3CD=5CE,3BC=5AC.
试说明：△ACD∽△ECF.
 |
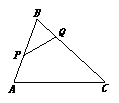9.如图，在△ABC中，AB＝8cm，AC＝16cm，点P从点A开始沿AB边向
B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的
速度移动，如果P、Q分别从A、B同时出发，经几秒钟△PBQ与
△ABC相似？