初二数学模拟测试
班级 姓名 成绩
一、填空题：（3分×8=24分）
1、
－π=__________.
2、若
，则ab=__________.
3、
，则a的值为__________.
4、比较大小：
（1）cos89°_________cos19° （2）cos10°_________sin20°.
5、已知一次函数y=－mx＋(m－2)，若它的图象经过原点，则m=_________；若图象经过一、三、四象限，则m的取值范围是__________.
6.一组数据：-1、0、2、-3、4的极差为 ，方差为
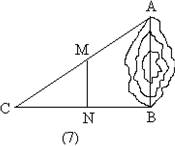
7．初三(1)班数学兴趣小组到野外实习测量：如图，AB两点被池塘隔开，在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN=15米，那么AB=________米。
8．已知y与x2成正比例，当x=－1时，y=2。则当y=6时，x=________。
9．已知三角形三个内角的度数之比为1∶2∶3，最小边的长是3cm，则这个三角形最大边的长是________cm
10．函数y=
中自变量x的取值范围是_________。
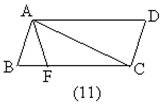
11．如图，已知平行四边形ABCD中，AB=2，AD=4，BF∶FC=1∶3，则⊿ABF与⊿ADC的面积比是________。
12、已知线段a=2cm，b=3cm，c=6cm，d是a、b、c的第四比例项，那么d= 。
13、如图，在菱形ABCD中，AE⊥BC于E，EC=1， sinB=
,则四边形AECD的周长=__________ 
二、单项选择题：（3分×8=24分）
14、下列语句中正确的是（ ）
A．带根号的数是无理数 B．不带根号的数一定是有理数
C．无理数一定是无限不循环小数 D．无限小数都是无理数
15、若点A关于x轴的对称点的坐标为（－1，2），则A点的坐标是（ ）
A．（－1，－2） B．（1，2）
C．（1，－2） D．（－1，2）
16、函数y=－3x＋4的图象不经过（ ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
17．下列四个函数中，当x>0时，随x增大而增大的函数是( )。
(A)
(B)y=－2x+1 (C)
(D)y=－2x－1
18、下列二次根式中与
是同类二次根式的是（ ）
A、
B、
C、
D、
19、下列命题中真命题是（ ）
A、两个直角三角形是相似三角形 B、两个等边三角形是相似三角形
C、两个等腰三角形是相似三角形 D、相似三角形面积的比等于它所对应的边的比
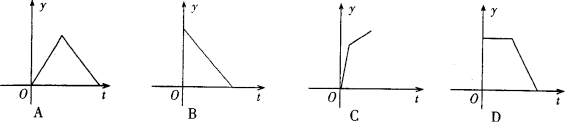
20、某产品的生产流水线每小时可生产100件产品，生产前没有产品积压，生产3h后安排工人装箱，若每小时装产品150件，未装箱的产品数量y是时间t的函数，这个函数的大致图象只能是下图中的（ ）
21、如果∠A为锐角，且cosA=
,那么（
）
A．0°<∠A
30° B．0°<∠A45°
C．45°<∠A60° D．60°<∠A90°
22、如图所示，下列每个图是由若干盆花组成的形如三角形的图案，每条边（包括两个顶点）有n盆花，每个图案花盆总数是S，按此推断S与n的关系式为（ ）
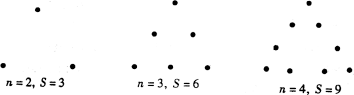
A．S=3n B．S=3(n－1)
C．S=3n－1 D．S=3n＋1
23、下列函数中自变量x的取值范围是x
2的是（
）
A．y=
B．y=
C．y=
D．y=
24、幸福村村办工厂今年前五个月生产某种产品的总量C（件）关于时间t（月）的函数图象如图所示，则该厂对这种商品来说（ ）
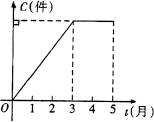
A．1月至3月每月生产总量逐月增加，4、5两月每月生产总量逐月减少
B．1月至3月每月生产总量逐月增加，4、5两月每月生产量与3月持平
C．1月至3月每月生产总量逐月增加，4、5两月均停止生产
D．1月至3月每月生产总量不变，4、5两月均停止生产
三、解答题
25、（6分）当k为何值时，函数y=(k2＋2k)
是正比例函数？
26、（6分）（1）若点（5－a,a－3）在第一、三象限角平分线上，求a的值；
（2）已知两点A（－3，m），B（n,4），若AB∥x轴，求m的值，并确定n的范围；
（3）点P到x轴和y轴的距离分别是3和4，求点P的坐标；
（4）已知点A（x,4－y）与点B（1－y,2x）关于y轴对称，求yx的值.
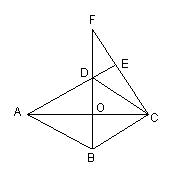
27．如图,菱形ABCD中,CF⊥AD,垂足为E,交BD的延长线于F．求证:AO2=BO•OF．
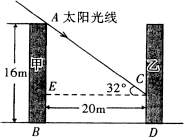
28、（8分）某房地产集团筹建一小区，居民楼均为平顶条式，南北朝向，楼高统一为16m（五层）.已知该城市冬至正午时分太阳高度最低，太阳光线与水平线的夹角为32°，如果南北两楼相隔仅有20m（如图所示），试求：
（1）此时南楼的影子落在北楼上有多高？（已知tan32°=0.6249）
（2）如按城市规划要求，使前后楼每层居民在冬天都能有阳光，两楼间的距离应是多少米？
29、（8分）如图（1）所示，四边形ABCD是一张矩形纸片，∠BAC=α
（0°<α45°），现将其折叠，使A、C二点重合.
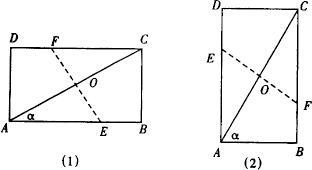
（1）作出折痕EF；
（2）设AC=x，EF=y，求出y与x之间的函数关系式；
（3）如图（2），当45°<α<90°时，（2）中求得的函数的关系式是否成立？若成立，请说明理由；若不成立，请求出当45°<α<90°时，y与x之间的函数关系式.
30、某商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元.该商场为促销制定了两种优惠办法.
A种办法:卖一支毛笔就赠送一本书法练习本;
B种办法:按购买金额打九折付款.
某校欲为校书法兴趣小组购买这种毛笔10支,书法练习本x(x
)本.
(1)写出每本优惠办法实际付款金额y(元)与x(本)之间的函数关系式;
(2)比较购买同样多的书法练习本时,按那种优惠办法付款更省钱;
(3)如果商场允许可以任意选择一种优惠办法购买,也可以同时用两种优惠办法购买.请你就购买这种毛笔10支和书法练习本60本设计一种最省钱的购买方案.
31、某农场300名职工耕种51公顷土地，分别种植水稻、蔬菜和棉花，种植这些农作物每公顷所需的职工人数及这些农作物每公顷的预计产值如下表所示：
| 农作物 | 每公顷所需人数 | 每公顷预计产值 |
| 水稻 | 4 | 4.5万元 |
| 蔬菜 | 8 | 9万元 |
| 棉花 | 5 | 7.5万元 |
设水稻、蔬菜、棉花的种植面积分别为x公顷、y公顷、z公顷
（1）用含x的代数式分别表示y和z；
（2）若这些农作物的总产值p满足关系360≤p≤370（x、y、z均为整数），求这个农场应怎样安排水稻、蔬菜、棉花的种植面积才能取得最优效益？