初二数学期末卷1
班级 姓名 学号 得分
一、填空题（每格2分，共26分）
1、 
已知
是二次函数， 则
__________.
2、 抛物线
在
轴上截得的线段长为__________.
3、 已知抛物线过点（6，0），且
时有最小值
，则
相应的二次函数的解析式是_____________.
4、已知：
则
5、
与
的比例中项是____________. （图１）
6、如图１，两平行线交∠A的一边于B、C两点，交∠A的另一边D、M 两
点，已知AC+AB=14，且AM：AD=4：3，则AB的长为___________.
7、线段AB上有一点C，分别以AC、BC为直径画圆，若AB=2cm，则
当AC=__________cm时，两圆面积和最小，最小值为___________cm
.
8、如果△ABC中，AB=AC，△DEF中，DE=DF，要使△ABC与△DEF相似，还需增加的一个条件是________________.（填上你认为正确的一个即可，不必考虑所有可能情况）
|
|
（图２） （图３） （图４）
10、如图２，在Rt△ABC中，∠C=90°，内接正方形GFED的边长为，若BE=9，AF=4，则
=_____________.
11、如图３，在平行四边形ABCD中，AB=4，BC=1，E是CD边上一动点，AE、BC的延长线交于点F，设DE=cm，BF=
cm，则与的函数关系式为_______________.
12、如图４，G是正六边形ABCDEF的边CD的中点，连结AG交CE
于点M，则GM ：MA=___________.
二、选择题（每题2分，共20分）
13、下列各组数成比例的是 （ ）
(A)1、
、4、
(B) 23、253、78、
(C)
、
、
、
(D)2、
、
、3
14、已知二次函数
，若＞0，则的取值范围是 （ ）
(A) ＞1 (B) ＜1 (C) 
(D)全体实数
15、二次函数
，其中
、
是常数，当达到最小
值时，的值为
( )
(A) 
(B) 
(C) 
(D)
16、已知
，下列判断正确的是
( )
(A)
(B) 
(C) 
(D)
17、直角三角形两条直角边之比是1：2，则它们在斜边上的射影之比为（ ）
|
(D)2 ：1
E A D
（图５） （图６） （图７） （图８）
18、如图５，在平行四边形ABCD中，E为CD上一点，DE ：CE=2 ：3，
连结AE、BE、BD，且AE、BD交于点F，则△DEF ：△EBF ：△ABF
为 ( )
(A) 4 ：10 ：25 (B) 4 ：9 ：25 (C)2 ：3 ：5 (D)2 ：5 ：25
19、如图６，D为△ABC边AC上一点，∠DBC=∠A，已知BC=，ΔBCD
与ΔABC的面积比为2 ：3，则CD的长是 （ ）
(A) 
(B) 
(C)
(D) 
20、 如图７，AD∥EF∥BC，AD=15, BC=21, 2AE=BE, 则EF的长( )
(A) 14 (B)15 （C）16 （D）1７
|
且BＥ=3ＥC，Ｆ是CD的中点，则
的值是（ ）
（A） 1 （B） 1.5 （C）2 （D）3
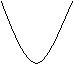
22、二次函数的图象如图９，那么
，
，
， -1 O 1
这四个代数式中，值为正数的个数为 （ ）
（A） 4（B） 3（C） 2 （D）1 （图９）
三、解答题和证明题（共54分）
23、（12分）已知抛物线
，根据下列条件，分别求
的值
（1） 对称轴是直线；
（2） 其最小值是
；
（3） 顶点在轴上；
（4） 顶点在直线
上．
24、（8分） 如图10，△ABC内接于⊙O, AD是直径，CE⊥AD，
求证：
（图10）
25、（6分）请设计三种不同的分法，将直角三角形（如图11）分割成四个小三角形，使每个小三角形与原直角三角形都相似（画图工具不限，要求画出分割线段，标出能够说出分法的必要记号，不要求证明，不要求写画法）
注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法
（图11）
26、（8分） 在△ABC中，D为BC边上的中点，E为边AC上任意一点，BE交AD于点O，某学生研究这一问题时，发现了如下事实：
(图12) (图13) (图14)
（1） 当时
，有
（如图12）
（2） 当时
，有
（如图13）
（3） 当时
，有
（如图14）
在图15中，当
时，参照上述研究结论，请你猜想用
表示
的一般结论，并给出证明（其中是整数）
(图15)
27、(10分)已知抛物线过A（
0），B（1，O），C（0，2）三点，
（1） 求这条抛物线的解析式；
（2） 在这条抛物线上是否存在一点P，使∠AOP=45°？若存在，请求出点P的坐标，若不存在，请说明理由.
28、（10分）如图16，梯形ABCD中，AB∥CD，P、M、N分别是AD、
AB、CD上的点，且PM∥BD，PN∥AC．
（１）
求证：
；
（２） 若AC⊥BD，AC＝BD＝12，并设PN＝x，△PMN的面积为y，求y与x的函数关系式；
（３）
在（２）中，当x取什么数值时，△PMN的面积最大？并指出此时点P在线段AD上的位置．
命题、校对：王波明、卢芳芳、邹锦丽
初二数学期末卷答案
一、填空题
（每格2分，共26分）
4、
-1 2、
3、
即
4、5：2 5、±1 6、6 7、1，
8、∠A=∠D等
9、100 10、6
11、
12、 1：6
二、选择题（每题2分，共20分）
13、C 14、C 15、C 16、C 17、B 18、A 19、B 20、D 21、C 22、B
三、解答题和证明题（共54分）
23、（12分）（1） 6
（2） 2或-6 （3） 0或- 4 （4）0或- 6
24、（8分）略
|
 | |||||
 | |||||
 | |||||
26、（8分）当时，=
，证明：略
27、（10分）（1）
（2） P（-1-，-1-）或P（-，）
28、（10分）（1）略
（2）
（
（3）
时，△PMN的面积最大，
此时点P在线段AD的中点．