初二数学期末自测题
（时间:90分钟 分数:120分）
一、填空题（每题3分，共30分）
1、若x3 =
—8a6b9,
则x=(
)
A
D
2、—3y2(1—1/3y + 2/3y2) = （ ）
3、a2+b2—_ab+( ) = (a + b) 2 B C
4、如图，平行四边形ABCD对角线AC与BD交于O，则图中全等三角形有（ ）对
5 若不等式(m-2)x>1的解集是x< , 则m 取值范围是_____
6 若多项式x2-px-6的一个因式是x-3,则p的值是____＿＿。
7、在正方形ABCD的边BC的延长线上取一点E，使CE=AC，AE与CD交于F，则∠AFC=＿。
8、若方程KX+1=2x-1的解是正数，则k的取值范围是＿＿＿＿＿＿。
9、一元一次不等式组（x+5）/2>1与4—x≥1的非负整数的解是（ ）。
10、若x2+kx+1/4、是一个完全平方式，则k=( )。
二、选择题（每题3分，共２４分）
1、由X＜Y得到aX＞aY的条件是
A：a ≥0 B：a ≤ 0 C： a＞0 D： a ＜0
2、不等式组x〈a与x〈b是x〈a，则（ ）
A、a〈b B、a〈b〈0 C、a〉b D、a ≤b
3、下列运算正确的是（ ）
Ａ、（xy2）3＝xy6 B、（3 xy2）2＝ 6x2 y2 C、（—2 x2）2 = —4x4 Ｄ、（x2 y3）m＝x2m y3m
4、如果不等式组
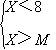有解，那么m的取值范围
A：m ＞8 B：m ≥8 C： m＜8 D：m≤ 8
5、已知M=8x2 －y2+6x－2,N=9x2 +4y2+13则M－N的值
A：为正数 B：为负数 C：为非负数 D：不能确定
6、下列命题中假命题是（ ）
A、全等三角形的对应高相等 B、三组对应角相等的两个三角形全等C、三边对应相等的两个三角形全等D、一条直角边和斜边对应相等的两个直角三角形全等
7、若a、b是有理数，则下列说法中正确的是 （ ） 。
A 若a>b则a2>b2 B 若a2>b2 则a>b C 若a>b则a2>b2 D 若a>b 则a2≠b2
8、顺次连结矩形各边中点所得四边形一定是（ ）
A、 一般平行四边形B、矩形C、正方形D、菱形
三、解答题(46分)
1、 计算 ( —22x )（—y）2 + 3xy（1— 1/3y）
2、 化简求值 （2a+3b）（2a—3b）+（a—3b）2，其中a = —5，b=1/3。
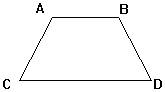
3、 如图AB∥CD，∠C=50度，∠D=80度，AB=4，DC=10，求BD的长。
4、 某城市的出租汽车起步价为10元(即行驶距离在5千米以内都需付10元车费)，达到或超过5千米后，每行驶1千米加1.2元(不足1千米也按1千米计)。现某人乘车从甲地到乙地，支付车费17.2元，问从甲地到乙地的路程大约是多少？
5、 
解不等式组并把解集在数轴上表示出来
2x — 6 ≤ 3x
x+2 x —1 ≥ 0
5
4
6、 已知不等式组
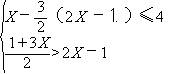
①解此不等式组，并把解集在数轴上表示出来。
②求此不等式组的非正整数解。
7某校初一年级四个班级200名学生中，有部分学生住宿在学校，在安排宿舍时，若每间住6人，则有5人住不下，若每间住8人，则有两间宿舍没人住。
问：宿舍共有几间？
四、作图题
一个边长为2厘米的等边三角形ABC，以点A为旋转中心，逆时针旋转45度得到ΔADE，
画出旋转后的图形.。
五、探究题
某学校计划购置一批电脑, 现有甲乙两个公司报价每台均为a元, 甲公司的优惠条件是购买10台以上, 则从第11台开始按报价70%的计算. 乙公司的优惠条件是每台按报价85%的计算, 如果电脑的品牌.质量和售后服务完全相同 ,你如何选择购货公司?