初二数学
第二学期期中考试试卷
（考试时间：120分钟；满分：150分） 成绩_______
一、填空题（每空2分，共40分）
1. 5的平方根为____________，
的算术平方根为____________.
2. 若一个n边形的外角和等于它的内角和的
，则n=_____，此n边形的对角线
有_______条。
3. 
，当ab＜0时，化简
=____________.
4. ABCD中，∠A－∠B=80º，则∠C=_______，∠D=_______.
5. 当a＜2时，化简
=________，计算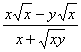
=________.
6. 比较大小：－4_______－
,
_______
.
7. 梯形的上底长为6cm，中位线长为9cm，则它的下底长为_______，两条对角线的
中点的距离为___________。
8. 若代数式
有意义，则x的取值范围是__________.
9. 方程
的根为____________.
10. 矩形的两条对角线夹角为60º，一条对角线与
短边的和为15，则长边的长为______.
11. 在△ABC中，AD⊥BC于D，AB、AC的中点分别为E、F，若AEDF为菱形，
则△ABC需满足条件_______________________（填写一个你认为适当的条件）
12. 已知关于x的方程
没有实数根，则k的取值范围是_____________.
13. 在四边形ABCD中，给出下列条件：① AB∥DC ② AD=BC ③ ∠B=∠D，
以其中两个条件作为题设，另一个作为结论，写出一个真命题是：_____________
___________________________________________________.
二、选择题（每题3分，共24分）
14. 下列根式：
；
；
；
；
；
中最简二
次根式的个数是（ ）
A. 2 B. 3 C. 4 D. 5
15. 在① 圆 ② 等腰梯形 ③ 正三角形 ④ 正方形 ⑤ 平行四边形中既是轴对称
又是中心对称的图形是（ ）
A. ① ② B. ③ ④ C. ① ④ D. ① ⑤
16. 下列说法正确的是（ ）
A. 2是－4的算术平方根 B. 对角线相等的四边形是矩形
C. 8的立方根是±2 D. 对角线互相平分的四边形是平行四边形
17. 四边形ABCD中，∠A、∠B、∠C、∠D的度数比为1∶2∶6∶3，则∠D等于（ ）
A.
60º B.
75º C.
90º D.
120º
18. 顺次连接四边形ABCD各边中点得四边形EFGH，
要使EFGH为菱形，应添加的条件是（ ）
A. AB∥CD B. AC=BD C. AB=CD D. AC⊥BD
19. 已知xy=
，x－y=
，则（x＋1）(y－1)的值为（ ）
A.
B. 
C.
D.
20. 矩形纸片ABCD沿DF折叠后，点C恰好落在AB边上的E点，
若∠ADE=30º，AB=6，则梯形ABFD的中位线长为（ ）
A. 
B.
C.
D.
不能确定
21. 若
，则
的值等于（ ）
A. 0 B. －1 C. －2002 D. －2001
三、解答题
22.（本题10分）
① 计算：
② 解方程：
23. 化简求值（本题12分）
① 已知
，求代数式
的值。
② 已知
，求
的值。
24.（本题6分）已知一元二次方程
的根是另一根的平方，求k的值。
25. 应用题（本题8分）新疆部分地区发生较强地震，某校甲、乙两班积极向灾区捐
款，恰好两班都捐了360元，已知：甲班比乙班多5名学生，乙班比甲班平均每
人多捐了1元，求乙班平均每人捐了多少元？
26. 证明题（本题6分）已知，梯形ABCD中AD∥BC，
M、N为两腰AB、CD的中点，ME∥AN交BC于E，
求证：AM=EN。
27.（本题8分）矩形ABCD中，AE⊥BD于E，若BC=6，∠CBD=30º，求CE的长。
 |
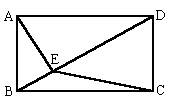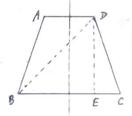
28. 作图题（本题8分）作一等腰梯形，使得上底为2cm，下底为4cm，高为3cm，（不写
作法，保留作图痕迹）并求出此梯形的腰长及对角线的长。
29.（本题8分）已知关于x的方程
有两个相等的实数根，
其中a、b、c是△ABC的三个角∠A、∠B、∠C的对边，
① 试判断△ABC的形状，并求出∠A的度数；
② 若方程的两个相等实根为时，求a∶b∶c的值。
30.（本题8分）已知关于x的一次方程
的根为－1，关于x的二次方程
的两实根分别为
、
，且
，求m、n的值。
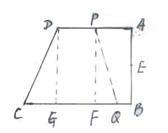
31.（本题12分）梯形ABCD中，AD∥BC，∠B=90º，AB=14cm，AD=18cm，BC=21cm，
点P从A点出发沿AD边以1cm/秒的速度向点D移动，点Q从C点出发沿CB边以
2cm/秒的速度向B点移动，且P、Q分别从A、C同时出发，移动时间为t秒
① t为何值时，梯形PQCD恰好为等腰梯形？
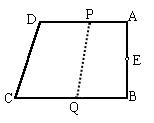② t为何值时，AB的中点E到PQ的距离为7cm？
命题、校对：郭长松
参考答案
一、填空题
1、
，3 2、6，9
3、4，-
4、1300，500
5、2a，
6、<
<
7、12，3
8、
9、x1=-2,x2=16
10、
11、AB=AC（或
）
二、选择题
14、A 15、C 16、D 17、C 18、B 19、B 20、A 21、B
三、解答题
22、（1）解：原式=
（2）解：原方程可化为：
23、（1）解：原式=
所以原式=
（2）解：解方程
原式=
原式=
24、解：设方程的根分别为a,a2
则a2+a=6 解得a1=2,a2=-3
当a=2时，k=
当a=-3时，
所以k的值为8或-27
25、解：设乙班平均每人捐3x元，乙班共有学生y人，则甲班平均每人捐3（x-1）元，甲班共有学生（y+5）人
所以
解：由（2）得 xy+5x-y=360+5 将（1）代入得
y=5x-5代入（1）得 5x2-5x-360=0即x2-x-72=0 所以x1=9 x2=-8
由题意知：x=9
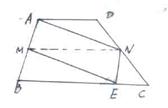26、证明：连结MN，因为M，N分别是AB，CD的中点，所以MN是梯形ABCD的中位线
所以AD//MN//BC 所以
又因为AN//ME
所以
因为AM=BM 所以
所以AN=ME 所以AMEN为平行四边形
所以AM=EN
27、解：因为四边形ABCD为矩形，所以BC=AD=6，
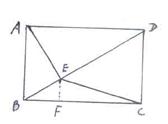在Rt
中，AE=3
在Rt
中，因为
过E作EF
于F，在
中，
所以
在Rt
中，
所以CE的长为
28、（1）作法略，图中梯形ABCD即为所作的梯形
（2）过D作DE垂直BC于E，因为ABCD为等腰梯形
所以
在Rt
CDE中，腰
连BD，因为BE=DE=3
在RtBDE中，对角线BD=
29、（1）解：由条件得 4b2-4(a+c)(a-c)=0
所以b2-a2+c2=0 所以b2+c2=a2
所以ABC为直角三角形且
（2）因为方程的两根x1=x2=
所以
所以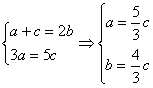
所以a:b:c=
30、解：因为x=-1是方程mx+n=1的根 所以-m+n=1 (1)
因为
所以
若
，则
将m=n-1代入得n2-4n+4=0 所以n=2,m=1
若
，则
，所以n=0，m=-1
综合以上情况可得m=1,n=2或m=-1,n=0
31、（1）因为AP=t，CQ=2t，要使PQCD为等腰梯形
分别过P、D作PF垂直BC于F，DG垂直BC于G，则CG=QF
因为CG=BC-AD=3 FQ=2t-(t+3) 所以t-3=3
所以t=6 答经过6秒钟，PQCD为等腰梯形。
（2）过E作EM垂直PQ于M，则EM=7
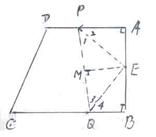即AE=BE=EM=7 连结PE、QE，则
所以
所以PM=PA；QB=QM
所以PQ=PA+BQ=t+(21-2t)=21-t
在RtPQE中，PQ2=PE2+QE2
即
化简得
解得t1=7,
答：经过3.5秒或7秒钟，E到PQ的距离为7cm