初二数学第二学期期中试卷4
成绩_____________班级_____________姓名___________
一、填空题：（本题共20分，每小题2分）
1、如果
，那么x=____________．
2、如果式子
在实数范围内有意义，那么实数x的取值范围是__________．
3、比较大小：
____2
．
4、如果一个多边形的每一个外角都等于30°，那么这个多边形是_________边形．
5、如果实数a、b在数轴上的位置如图所示，那么化简
=______________．
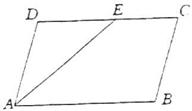
6、
ABCD中，∠A的平分线AE交DC于E，如果∠DEA=25°，那么∠B=_______°．
7、当a_________时，
．
8、有一个边长为11cm的正方形和一个长为15cm，宽为5cm的矩形，要作一个面积为这两个图形面积之和的正方形，则此正方形边长应为__________cm．
9、量得地图上A、B两地的距离是160mm，如果比例尺是1∶10000，那么A、B两地的实际距离是_____________m．
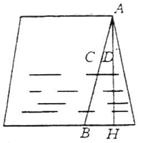
10、一井深AH为9米，一人用一根长10米的竹竿AB一头B插入井底，另一头A正好到井口，抽起竹竿量得浸入水中的长度CB为6米，则井中水的深度DH=__________米．
二、选择题：（本题共30分，每小题3分）
下列各题均有四个选项，其中只有一个是正确的．
1、和数轴上的点成一一对应关系的是（ ）．
（A）有理数 （B）无理数 （C）实数 （D）整数
2、下列图形中，既是轴对称图形，又是中心对称图形的是（ ）．
（A）平行四边形 （B）矩形 （C）等腰梯形（D）等边三角形
3、若最简二次根式
与
是同类二次根式，则x的取值为（ ）
（A）1 （B）0 （C）-1 （D）1或-1
4、如果
，那么x的值是（ ）．
（A）2和8 （B）2和-8 （C）-2和8 （D）-2和-8
5、顺次连结等腰梯形各边中点，所得的四边形一定是（ ）．
（A）矩形 （B）菱形 （C）正方形 （D）梯形
6、把
在实数范围内分解因式，结果正确的是（ ）．
（A）
（B）
（C）
（D）
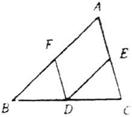
7、△ABC中，D、E、F分别是BC、CA、AB边的中点，那么四边形AFDE的周长等于（ ）．
（A）AB+AC （B）AD+BC （C）
（D）BC+AC
8、如果二次根式
有意义，那么x的取值范围是（ ）．
（A）x>-3 （B）x>3 （C）x<-3 （D）x<3
9、下列命题中，不正确的是（ ）．
（A）一个四边形如果既是矩形又是菱形，那么它一定是正方形
（B）有一个角是直角，且有一组邻边相等的平行四边形是正方形
（C）有一组邻边相等的矩形是正方形
（D）两条对角线垂直且相等的四边形是正方形
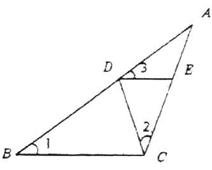
10、如图，△ ABC中，D、E分别为AB、AC上的点，如果∠1=∠2=∠3，那么图中的相似三角形共有（ ）对．
（A）2 （B）3 （C）4 （D）5
三、计算下列各题：（本题共24分，每小题4分）
1、
； 2、
；
解： 解：
3、化简
（x>1） 4、已知：
，求
的值．
解： 解：
5、已知：ab=1且a=
， 6、已知：
，
求：（1）b的值； 求：x+3y的平方根．
（2）
的值； 解：
解：
四、（本题共12分，每小题4分）
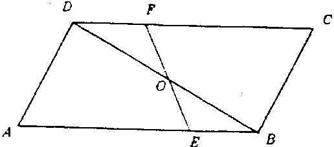
1、已知：如图，平行四边形ABCD中，E、F分别为AB、CD上的点，且AE=CF，EF与BD交于点O．
求证：OE=OF．
证明：
2、已知：如图，梯形ABCD中 ，AB∥CD，中位线EF长为20，AC与EF交于点G，GF-GE=5．
求AB、CD的长．
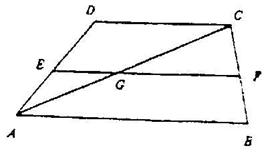
解：
3、已知矩形ABCD的一条对角线长为8cm，两条对角线的一个夹角为60°，求矩形的边长．
五、（本题7分）
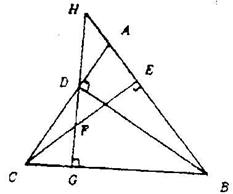
已知：如图，BD、CE是△ABC的高，DG⊥BC与CE交于F，GD的延长线与BA的延长线交于点H．
求证：
证明：
六、（本题7分）
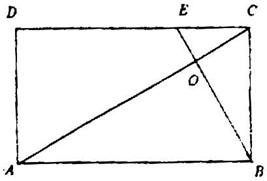
如图，E是矩形ABCD的边CD上的一点，BE交AC于点O，已知△OCE和△OBC的面积分别为2和8．
（1）求△OAB和四边形AOED的面积；
（2）若BE⊥AC，求BE的长．
解：
期中初二数学试卷
答案
成绩_____________班级____________姓名____________
一、填空题：（本题共20分，每小题2分）
1、±2； 2、x≥2； 3、＜； 4、十二； 5、-ab； 6、130； 7、≥1； 8、14；
9、1600；10、5.4．
二、选择题：（本题共30分，每小题3分）
1．C 2．B 3．A 4．C 5．B 6．D 7．A 8．D 9．D 10．C
三、计算下列各题：（本题共24分，每小题4分）
1．解：原式
2．解：原式
=24-25
=-1
3．解：原式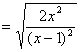
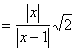
4．解：设：
则
5、（1）
（2）
=12
6、解：由已知得 
………………………… 1′
解得 
……………………………… 2′
∴x+3y=3+2×3=9 ……………………………… 3′
∴x+3y的平方根是±3 ……………………………… 4′
四、（本题共12分，每小题4分）
1．证明：在ABCD中，
∵AB∥CD
∴
1=2 ……………………………………………… 1′
∵AB=CD
AE=CF
∴AB-AE=CD-CF
∴BE=DF ……………………………………………… 2′
在△BOE和△DOF中
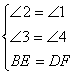
∴△BOE≌△DOF ……………………………………………… 3′
∴OE=OF ……………………………………………… 4′
2、解：在梯形ABCD中，AB∥CD，
∵中位线EF长为20
∴GF+GE=20
又∵GF-GE=5
解得 GF=
，GE=
………………………… 1′
∵EF∥AB∥CD
∴G为AC中点 …………………………… 2′
∴AB=2GF=25
CD=2GE=15 …………………………… 4′
3、解：
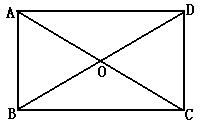
如图，矩形ABCD中，∠AOB=60°，AC=8cm
∴BD=AC=8cm
∴
……………………………… 2′
∴AO=BO
∴△AOB为等边三角形
∴AB=AO=4cm ……………………………… 3′
∵∠ABC=90°
∴BC
（cm）
∴矩形边长为4cm和
cm ……………………………… 4′
五、（本题7分）
证明：∵BD⊥AC，DG⊥BC
∴△CGD∽△DGB
∴
∴
……………………………… 2′
∵CE⊥AB
∴∠1+∠CBE=90°
又∠2+∠GBH=90°
∴∠1=∠2 ……………………………… 4′
∠FGC=∠HGB=90°
∴R+△CGF∽R+△HGB …………………………… 5′
∴
∴GF·GH=BG·GC …………………………… 6′
∴ …………………………… 7′
六、（本题7分）
解：
（1）∵△COE与△OBC中边EO，BO在同一直线上且此边上的高相等
∴
…………………………… 1′
在矩形ABCD中
∵DC∥AB
∴△OCE∽△OAB
∴
∴
………………………… 2′
∴
=
=8+32=40
∵AB=CD，BC=DA且∠ABC=∠ADC=90°
∴
=
∴
=40-2=38 …………………………… 4′
（2）设OE=x（x＞0）则
OB=4x BE=5x
在Rt△BOE中
∵∠BCE=90°，CO⊥BE
∴△COE∽△BOC
∴
………………………… 5′
∴CO=2x
∵
=
∴
∴
(负值舍去) ……………………………… 6′
∴
……………………………… 7′