初二数学第二学期期末复习试卷
第一部分
一、填空：（2′×25=50′）
1．
4的平方根是
，
的算术平方根是 。
2．
的相反数是 ，
的倒数是 ，
。
3．
当x=
时，
无意义，当x
时，
有意义，当x 时，
的值为0。
4．
化简：
，
。
5．
在实数范围内分解因式：
。
6．
方程
的根为
，分母有理化：
7．
方程
的判别式△= ，此时方程根的情况是 。
8．
方程
的一个根为2，则另一个根为 ，k= 。
9． 如果一个多边形的每一个外角都比内角少60°，则这个多边形的边数是 。
10．当矩形的面积为两对角线积的一半时，这个矩形的两邻边之比为 。
11．梯形ABCD中，AD∥BC，EF为中位线，当△AEF的面积为3时，则梯形ABCD的面积为 。
12．已知
，则k= 。
13．已知O是Rt△ABC的斜边AB的中点，DO⊥AB交AC于点D，AC=6，BC=3，则AB= ，OD= ，S△AOD∶S△ACB= 。
14．村办公室会计小马经常要画表格，已知平行线AB和CD之间距离为11cm，而要求AB和CD之间划出13个格子，小马用几何学原理这样画表格：先把直尺略斜放，使AB、CD之间放下13cm长的刻度，标出每隔1cm的分点，然后过这些分点画平行于AB的直线，小马说这个表格的画的过程，实质上应用了几何中的
定理。
二、选择：（2′×5=10′）
1．已知
，则
。（ ）
（A）±2（B）±4（C）2（D）4
2．甲乙两同学对代数式
（x＞0，y＞0）分别作了如下化简：
甲：原式=
乙：原式=
关于这两种化简过程的说法正确的是（ ）
（A）甲乙都正确（B）甲乙都不正确（C）只有甲正确（D）只有乙正确
3．下列图形中，有且仅有两条对称轴的图形是（ ）
（A）正方形（B）菱形（不含正方形）（C）等腰梯形（D）等边三角形
4．如图，已知ED∥BC，CD与BE相交于点O，△DOE与△COB的面积之比为4∶9，则AE∶EC为：（ ）
（A）2∶1（B）2∶3（C）4∶9（D）5∶4
5．如图：四边形ABCD为正方形，过A点的直线依次与BD、DC、BC的延长线交于E、F、G，已知AE=5cm，EF=4cm，则FG的长等于（ ）
（A）2cm（B）3cm（C）
cm（D）
cm
三、计算：（4′×3=12′）
1．
2．
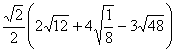
3．
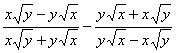
四、求值：（4′×2=8′）
1．化简求值：当x=2，y=6时，求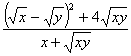
的值。
2．已知菱形ABCD的边长为3，延长AB到E，使BE=2AB，连EC并延长交AD的延长线于F。求AF的长。
五、证明：（6′×2=12′）
1．过平行四边形ABCD的顶点A作一条直线，分别交DB、CB、CD的延长线于E、F、G。求证：AE∶EF=EG∶AE。
2．过△ABC的顶点B、C分别作AB、AC的垂线BD与CD，两线交于点D，由C作CE⊥AD交AB于E。求证：∠AEF=∠ACB。
六、已知菱形ABCD中，AE、CF是BC、AD边上的高，且交对角线BD于G、H，若四边形AECF的面积为
，菱形ABCD的面积为
。求线段GH的长。（6′）
七、△ABC中，AB∶AC=3∶2，D在AB上，E在AC的延长线上，BD∶CE=4∶3，DE交BC于点F。求DF∶EF的值为多少？（6′）
第二部分
一、填空：（2′×4=8′）
1．观察下列各式：
，
，
，……
请你用一种字母表示出它的规律 。
2．用“CZ1206型计算器”求的值，在显示出DEG之后的按键顺序为 。
3．在△ABC中，BC=3AC，且∠B=∠EFA=∠FAC，△ABC的面积为S，△BEF的面积为S1，△ACF的面积为S2，则S1+S2= S。
4．在菱形ABCD中，∠BAD=60°，E为AB边上一点，且AE=3，BE=5，在对角线AC上找一点P，使PB+PE最小，此时PB+PE的值为 。
二、解答题：（6′+6′+6′=18′）
1．有一架不等臂的天平，某同学在用这架天平做实验时，很巧合地发现，当他把物体A、B放在左盘，C放在右盘；或把B、C放在左盘，A放在右盘；或把A、C放在左盘，B放在右盘时，天平都能平衡，接着他把物体D放入左盘称得为400克，请你用我们所学的数学知识解出把物体D放入右盘时，称得的质量为多少？
2．如图，A、B两个村子在河CD的同侧，A、B两村到河的距离分别为AC=1km，BD=3km，两村距离AB=
km，现要在河边CD上建一个水厂向两村输送自来水，铺设水管的工程费用为每千米2万元，请你在CD上选择水厂的位置O，使铺设水管的费用最小，并求出铺设水管的总费用F。
3．如图1，已知△ABC中，AB=AC，∠A=90°，AD=2BD，EC=2AE。
求证：∠ADE=∠EBC。
证明：作EF⊥BC于点F。
∵AB=AC
不妨设AB=AC=3k
∵AD=2BD，EC=2AE
∴AD=2k，AE=k，EC=2k
∵∠A=90° ∴ ∠C=45°且BC=
∴EF=FC=
∴ BF=
即
又∵∠A=∠BFE
∴△ADE∽△FBE∴∠ADE=∠EBC
根据上题的解题思路和方法，试解答下述问题：
如图2，△ABC中，AB=AC，∠A=120，点D、E分别在AB、AC上，AB=2AD，∠ADE=∠EBC，求：AE∶EC的值。