初二年级三角形相似和判定定理
[本周教学内容]
1． 掌握相似三角形的有关概念；
① 
.相似三角形：对应角相等，对应边成比例的三角形，叫做相似三角形。相似三角形对应边的比叫做相似比（或相似系数），若△ABC与△AˊBˊCˊ的相似比为K1，△AˊBˊCˊ与△ABC的相似比为K2,则有
；当且仅当△ABC≌△AˊBˊCˊ时，才有K1
=K2。
②.定理：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。
2．掌握三角形相似的判定定理1。
1判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似（简写成两角对应相等，两三角形相似。）
2判定定理2，如果一个三角形的两条边和另一个三角形的两条边对应成比例。并且夹 角相等，那么这两个三角形相似。（简：两边对应成比例且夹角相等，两三角形相似）
3判定定理3：如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似（简写成：三边对应成比例，两三角形相似）
4定理：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。
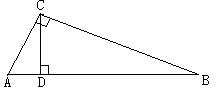5直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
如图：Rt△ABC中，CD是斜边上的高。
则：△ABC∽△CBD∽△ACD.
[本周教学的重难点]
重难点：正确理解相似三角形的相似比,三角形相似的判定定理。
[练习题]
一、
填空题。
1、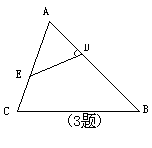
△ABC和△DEF的相似比为 ，则△DEF与△ABC的相似比为 ；若△ABC和△DEF的相似系数1，则△ABC △DEF；
2、如图，△ABC∽△ADE，
且DE∥BC则对应边的比例式为 ；
3、如图，ABC中，D .E分别是AB . AC上的点，
且∠ADE=∠C，则△AED △ABC，对应边的比例式为 ，
对应角为：
;
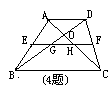
4、已知：如图，梯形ABCD中， AD∥BC,AC .BD相交于点O，
中位线EF分别交AC.BD于H.G，
则△AEH∽ △ACD∽ △OGH∽ ∽ ;
5、如图，CD是Rt△ABC斜边上的高，则△ADC和△BDC的对应边的
比例式为 ，Rt△ABC和△ADC的对应边的比例式为 ；
6、已知△ABC∽△EFG，若∠A=72°∠F=48°，则∠C= 度。
二、选择题：
1、
△ABC三边长分别为 , , 2 ，△AˊBˊCˊ的三边长分别为1， 和X，若△ABC∽△AˊBˊCˊ，则X＝（ ）
A
B 2 C D 2
2、△ABC∽△AˊBˊCˊ，若BC＝3，BˊCˊ＝1.8,则△AˊBˊCˊ与△ABC的相似比为（ ）
A 5:3 B 3:2 C 2: 3 D 3:5
三、解答题：
1、已知：如图，△ABC中，D为BC上一点，且∠BAC=∠ADC,BC=16,AC=12。
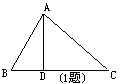求：CD的长。
2、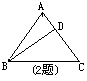
已知：如图：△ABC中，AB=AC,D是AC上一点，BD=BC
求证：BC2 =AC·CD
3、已知：如图，梯形ABCD中，AD∥BC，∠BAD=90°，对角成BD⊥DC。
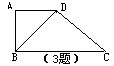求证：（1）△ABD∽△DCB
（2）BD2 =AD·BC
4、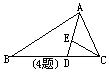
已知：如图△ABC中，AD是角平分线，CD=CE
求证：AE·BD=AD·CD
[练习题]
一． 填空题：
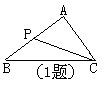
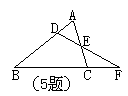
1． 
如图△ABC中，P是AB上一点，连接CP，当∠ACP=
或 = 时，△ACP∽△ABC；
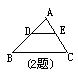
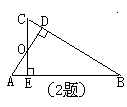2．如图：AD⊥BC、CE⊥AB，图中有 对，相似三角形
 |
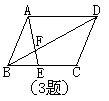3．在 ABCD中，E是BC上的一点，AE交BD于F，若BE:EC=4:5，
则BF:FD= ；
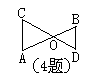
4.如图,能使△AOC∽△BOD成立的一个条件是
；
5．如图，能使△ABC∽△ADE的一个条件是 ；
二． 选择题：
1． 下列各组图形必相似的是（ ）
A.各有一个角是400的两个等腰三角形 B.两条边之比是2:3的两个直角三角形
C.各有一个角是1000的两个等腰三角形 D.任意两个等腰三角形
2.下列命题是假命题的是( )
A. 有一个底角相等的等腰三角形相似 B.两个全等三角形相似
C.两个等边三角形相似 D.有两边和一角对应相等的两个三角形相似
3.根据下列条件, △ABC和△A′B′C′不相似是（ ）
A．∠A=∠A′=680， ∠B=400，∠C′=720
B．∠B=∠B′，BC:A′B′=AB:B′C′
C.AB=6,BC=9,AC=12, A′B′ =18,B′C′=27,A′C′=36
D.AB=3,AC=2,A′B′=12,A′C′=6,∠C=∠C′=900
三.判断题:(对的划√错的划×)
1．△ABC和△A′B′C′中，a=5，b=4，c=2.5，a′=25，b′=10，c′=8，
则△ABC∽△A′B′C′（ ）
2．有一个角相等的两个等腰三角形相似（ ）
3．△ABC中，∠C=900，AB=6cm，AC=4cm，△A′B′C′中，∠C′=900，A′B′=1.8cm,
A′C′=1.2cm,
则△ABC∽△A′B′C′ ( )
4．在△ABC和△A′B′C′中，∠A=800，∠B=400，∠A′=800，∠B′=600， 则△ABC∽
△A′B′C′（ ）
四，解下列各题：
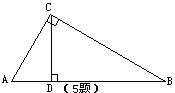
1．如图，△ABC中，∠ACB=900，CD⊥AB于D若DB= ，
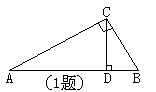求：AC、BC的长
2． 已知：如图，Rt△ABC中，∠B=900，AB=BE=EF=FC，
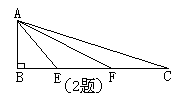求证：△AEF∽△CEA
3． 已知：如图，四边形ABCD中，∠A=∠CBD，AB=4cm，AD=6cm，BD=5cm，BC=7.5cm
求：CD的长
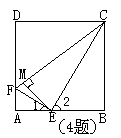
4． 已知：如图，在正方形ABCD中，E为ABCD中点，F为AD上一点，AF:DF=1:3
EM⊥FC,求证:(1) ∠1+∠2=900 (2)EM2=MF.MC
 |