初二全等三角形复习卷
一、填空题：
1.判定一般三角形全等的方法有 等四种，判定直角三角形全等的方法还有
.
 |
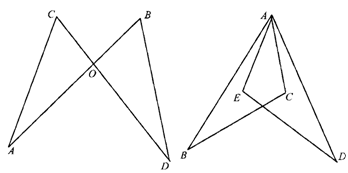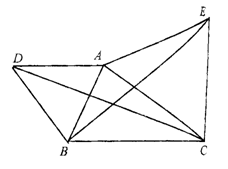
2.如图1-2-18，已知△OCA≌△OBD，C和B、D和A是对应顶点，这两个三角形中相等的角是 ，相等的边是 .
图1-2-18 图1-2-19
3.△ABC的角平分线AM、BN交于I点，那么I点到 边的距离相等，连结CI，那么CI一定平分 .
 |
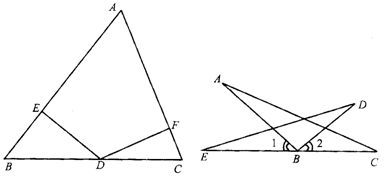4.如图1-2-19，已知△ABC≌△ADE，∠B与∠D是对应角，那么AC与 是对应边，∠BAC与 是对应角.
图1-2-20 图1-2-21
5.如图1-2-20，已知D在BC边上，DE⊥AB于E，DF⊥AC于F，DE=DF，∠B=50°，∠C=70°，那么∠DAF= ，∠ADE= .
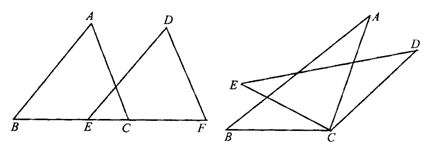6.如图1-2-21，已知AB=BE，BC=BD，∠1=∠2，那么图中
≌
，AC=
，∠ABC=
.
图1-2-22 图1-2-23
7.到一个角两边距离相等的点，在 .
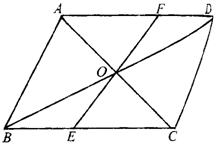
8.如图1-2-22，已知△ABC≌△DEF，对应边AB=DE， ，对应角∠B=∠DEF， .
9.如图1-2-23，已知△ABC≌△DEC，其中AB=DE，∠ ECB=30°，那么∠ACD= .
二、选择题
11.根据下列条件，能判定△ABC≌△DEF的是 .
A.AB=DE，BC=EF，∠A=∠D
B.∠A=∠D，∠C=∠F，AC=EF
C.∠B=∠E，∠A=∠D，AC=EF
D.AB=DE，BC=EF，∠B=∠E
12. 如图1-2-24，已知AB∥DC，AD∥BC，BE=DF，图中全等三角形有 .
A.3对 B. 4对
 |  | ||
C.5对 D.6对
图1-2-24 图1-2-25
13.如图1-2-25，已知△ABD和△ACE都是等边三角形，那么△ADC≌△ABE的根据是 .
A.边边边 B.边角边 C.角边角 D.角角边
14.具有下列条件的两个三角形，可以证明它们全等的是 .
A.两角相等，且其对应角所对的边也相等
B.两角相等，且有一边也相等
C.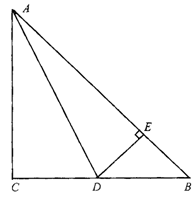
一边相等，且这边上的高也相等
D.两边相等，且其中一条对应边的对角相等
15.如图1-2-26，已知在△ABC中，∠C=90°，AC=BC，
AD平分∠CAB交BC于D，DE⊥AB于E，AB=8cm，
那么△DEB的周长为 .
A.4cm
B.4
cm
C.6cm D.8cm
图1-2-26
16.在△ABC和△A'B'C'中，①AB=A'B'，②BC=B'C'，③AC=A'C'，④∠A=∠A'，⑤∠B=∠B'，⑥∠C=∠C'，则下列条件组不能保证△ABC≌A'B'C'的是 .
A.①②③ B.①②⑤
B.②④⑤
D.①③⑤
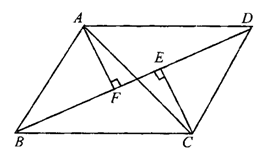
17.如图1-2-27，◇ABCD中，两对角线AC，BD交于点O，AF⊥BD于F，CE⊥BD于E，则图中全等三角形的对数共有 .
A.5对
B.6对
C.7对
D.8对
18.下列命题中正确的个数为 .
Ⅰ顶角和底边对应相等的两等腰三角形全等.
Ⅱ有一直角边和斜边对应相等的两Rt△全等.
Ⅲ有两边和其中一边上的高对应相等的两三角形全等.
A.3 B.2 C.1 D.0
三、解答题：
19.如图1-2-28，已知∠A=∠B，CE⊥AB，DF⊥AB，垂足分别为E、F，AD=BC.
求证：AE=BF.
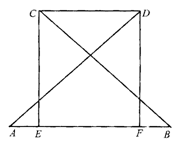
图1-2-28
20.如图1-2-29，已知M是△ABC的边BC上一点，BE∥CF。BE=CF.
求证：AM是BC边上的中线.
21.如图1-2-30，已知AB=DC，AE=DF，CE=BF.
求斑点：AF=DE.
22.如图1-2-31，已知在△ABC中，∠C=90°，两个锐角平分线AD、BE交于点O，∠1=60°.
求：∠AOB和∠ADC的度数.
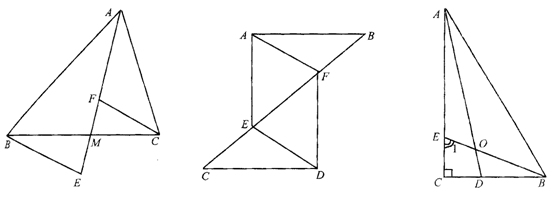
图1-2-29
图1-2-30
图1-2-31
23.如图1-2-32，已知BO=OC，AB=DC，BF∥CE，且A，B，C，D四点在同一直线上.
 |
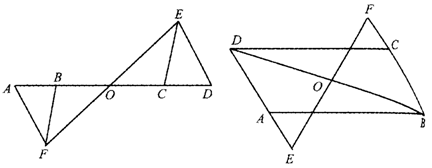求证：AF∥DE.
图1-2-32 图1-2-33
24.如图1-2-33，已知AB=DC，AD=BC，O是BD的中点，过O的直线与AD、BC延长
线分别相交于E，F.
求证:OE=OF
25已知如图1-2-34,AD=BC,AB=DC.
求证：∠A+∠D=180°
26.如图1-2-35，在△ABC中，AD为BC边上的中线.
求证：2AD<AB+AC.
27已知如图1-2-36，梯形ABCD中，AD∥BC，AB=DC，在AB、DC上各取一点F、G使BF=CG，E是AD的中点.
求证：∠EFG=∠EGF
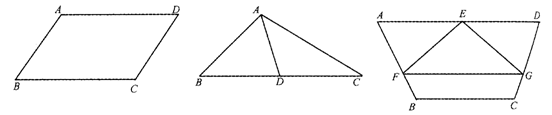
图1-2-34 图1-2-35 图1-2-37-6