初二数学试卷
班级： 学号： 姓名：
一、 填空题（每空1分，共17分）
1、实数0.000196的平方根是 .
2、
＝0.4，则
＝
.
3、
＝0.4，则＝
.
4、若
＝225，则＝
.
5、
的平方根是
.
6、
＝
.
7、－0.19是 的负的平方根.
8、比较大小：
.
9、直线
不经过第
象限.
10、双曲线
不经过第
象限.
11、把直线
向下平移4个单位，得到直线
.
12、已知点P到轴及
轴的距离都是1，则点P的坐标是
.
13、已知直线
、
、
相交于一点，则
＝ .
14、一次函数
的图象与直线
平行，且与直线
的交点在轴上，则
，
.
15、点P（，
）关于轴对称的点的坐标是
，关于原点对称的点的坐标是
.
二、选择题（每小题2分，共30分）
1、
＝
，则的取值范围是（ ）
A、
B、
C、
D、
2、当
时，化简
等于（ ）
A、
B、
C、
D、
3、下列各组二次根式中，字母都表示正数，各组内不是同类二次根式的是（ ）
A、
，
，
B、 
，
C、
，
，
D、
，
，
4、已知点P（－3，1），则点P关于轴对称的点的坐标是（ ）
A、（3，1） B、（－3，－1） C、（3，－1） D、（1，－3）
5、直线不经过（ ）
A、 第一象限 B、第二象限 C、第三象限 D、第四象限
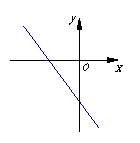6、直线如右图所示，则
、的符号是（ ）
A、
，
B、，
C、
，
D、，
7、正比例函数
的图象过点（－1，3），则为（ ）
A、
B、
C、3
D、－3
8、下列说法中，不正确的是（ ）
A、－1的平方是1 B、－2的立方是－8
C、－8的立方根是－2 D、1的立方根是－1
9、已知
，化简
等于（ ）
A、0 B、
C、
D、
10、下列函数中，随增大而增大的是（ ）
A、
B、
C、
D、
11、已知
是正比例函数，且随增大而减小，则解析式为（ ）
A、
B、
C、
D、
12、
与
在同一坐标系中的图象是（ ）
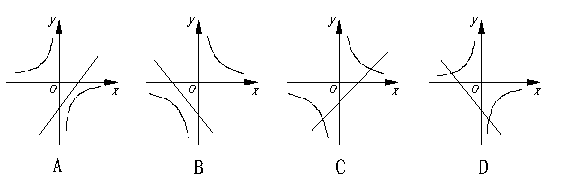
13、
和
（
）在同一直角坐标系中的图象是（ ）
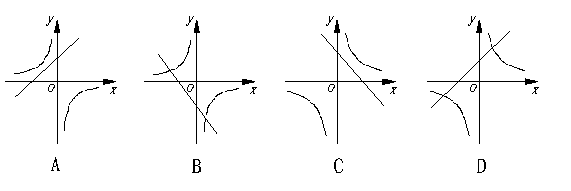
14、如果是的正比例函数，是
的一次函数，那么是的（ ）
A、正比例函数 B、一次函数
C、正比例函数或一次函数 D、不构成函数关系
15、如果点M（－3，
）在第三象限内，那么的取值范围是（ ）
A、
B、
C、
D、
三、判断正误（每小题1分，共13分）
1、0的平方根是0. （ ）
2、1的平方根是1. （ ）
3、1的平方根与1的立方根相等. （ ）
4、
＝±5.
（ ）
5、
的算术平方根是.
（ ）
6、3.1＜
＜3.2.
（ ）
7、数轴上的任意一个点，都表示唯一的一个实数. （ ）
8、坐标平面内的任意一个点，都可以用一个实数对来表示. ( )
9、无理数可分为正无理数，零，负无理数. （ ）
10、无理数都是开方开不尽的数. （ ）
11、若
，则
.
（ ）
12、式子叫做一次函数.
（ ）
13、带根号的数都是无理数. （ ）
四、按提示中的意图计算（共6分）
1、
求
的平方根. （3分）
解：∵
∴
即
2、求
的立方根. （3分）
解：∵
∴ 即
五、（共26分）
1、分解因式：
（5分）
2、计算：（
）（
） （5分）
3、实数，在数轴上的位置如图，化简：（5分）
4、已知
，
，求
的值. （5分）
5、已知一次函数的图象过点（1，1）和（―1，―5），求它的解析式，并画出函数图象.
（6分）
六、已知等腰三角形的周长为20cm.
1、写出底长与腰长的函数关系式； （2分）
2、写出自变量的取值范围； （2分）
3、画出函数的图象. （4分）