初二数学文化素质测试
一、细心填一填:可别填错啦!（1至14题每空1分,15至18题每空2分,本大题满分37分）
1、
16的平方根是 ，
的算术平方根是
，—8的立方根是 。
2、
=
，
=
。
3、函数y=
中自变量x的取值范围是
，y=
中自变量x的取值范围是
.
4、化简：
=
，试写出一个与它是同类二次根式的二次根式是
。
5、
无理数，
是
无理数。（填“是”或“不是”）
6、
的相反数是
，
的倒数是
。（要求分母不含根号）
7、点Q（2，
—3）关于 x轴对称的点的坐标为
，
关于y轴对称的点的坐标为 。
8、点P（—2，3）在第 象限，点Q（—7，0）在 轴上。
9、直线y= —x—3向上平移3个单位后得到直线 ， 然后再向右平移7个单位后得到直线 。
10、函数y=x+3的图象与x轴的交点坐标是 ， 与y轴的交点坐标是 。
11、已知函数y=2x—3，当x=2时；y= ；当y= —2时，x= 。
12、正比例函数y=kx（k≠0），当k<0时，图象过第 象限，y随x的增大而 。
13、若点（2，m），（—1，n）在函数y= —2x+1的图象上，则m= ；n= 。
14、若一次函数y=kx+b的图象不经过第一象限，则k 0，b 0。
15、若
=1 — a，则a的取值范围是
。
16、若
（x — 3）
+
=0，则x+y=
。
17、函数y=x+2m和y=4 — 2x与y轴交于同一点P，则m的值为 。
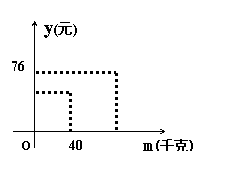18、小王以每千克0.8元的价格从市场购进若干
千克番茄去销售，在销售了一部分之后，
|
金额y（元）与卖番茄的千克数m之间的关
系如图所示，那么小王至少赚了 元。
二、精心选一选：可别张冠李戴哦！（每题3分，本大题满分21分）
19、对于叙述：“
的平方根是±
”，下列表达式正确的项是（ ）
A、
=
B、±= C、= D、±=
20、下列计算正确的是（ ）
A、
1+
=
B、
=
C、
=
D、
=3+4=7
21、将a
化成最简形式是（ ）
A、
B、
C、—
D、
22、函数y=kx+b经过第一、二、三象限，则的值（ ）
A、k>0 , b<0 B、k>0 , b>0 C、k<0 , b>0 D、k<0 , b<0
23、一次函数y= —2x — 3不经过的象限是（ ）
A、第一象限 B、第二象限 C、第三象限 D、第四象限
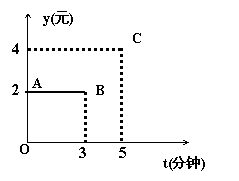
24、如图中的折线ABC，为甲地向乙地打长途电话所需付的电话费y（元）与通话时间t（分钟）之间的函数关系的图象，则通话7分钟需付电话费为（ ）
A、
2元
B、4 元
C、 6元 D、8元
|
25、设x，y为非零实数，则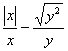
的所有可能值为（ ）
A、±1或0 B、±2或0 C、±1或2 D、±1或±2
三、耐心答一答，你一定是学习的智者！（本大题共42分）
26、计算：（每题3分，满分12分）
（1）
（2）
（3）
（4）
27、（本题满分4分）已知x — 2的平方根为±2，2x+y+7的立方根为3，
求：x+y的平方根。
28、（本题满分4分）已知一条直线经过点A（— 2，4），且与直线y=
平行，
（1） 试求出这条直线的函数关系式。（2分）
（2） 试判断点P（4，7）是否在这条直线上？并说明理由。（2分）
29、（本题满分6分）已知函数y=2x — 4的图象与x轴的交点是A，与y轴的交点为B。
（1）画出该函数图象。（2分）
（2）求出A点、B点的坐标。（2分）
（3）求出该直线与坐标轴围成的三角形面积。（2分）
30、（本题满分8分）某影碟出租店开设两种租碟方式：一种是零星租碟，每张收费1元；另一种是会员卡租碟，办卡费每月12元，租碟费每张0.4元，小彬经常来该店租碟，若每月租碟数量为x张，
（1）写出零星租碟方式应付金额y
（元）与租碟数量x（张）之间的函数关系式；(2分)
（2）写出会员卡租碟方式应付金额y
(元)与租碟数量x（张）之间的函数关系式；（2分）
（3） 小彬选取哪种租碟方式更为合算。（4分）
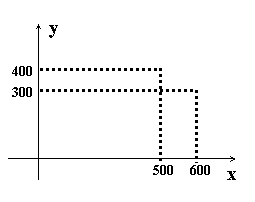
31、（本题满分8分）某公司试销一种成本单价为400元/件的新产品，规定试销时的销售单价不低于成本单价，又不高于700元/件，经试销调查，发现销售量y(件)与销售单价x（元/件）可近似看做一次函数y=kx+b的关系。
（1）根据图象求一次函数解析式；（2分）
（2）设公司获得的毛利润（销售总价一成本总价）为p元；
①试用销售单价x表示毛利润p；（2分）
②当销售单价定为每件650元时，该公司可获毛利润多少元？
此时的销售量是多少？（4分）
|