初二数学辅导课（4）
一、填空题
1、等腰三角形两腰上的高相等，这个命题的逆命题是 。
2、如果三角形的三边长分别是7、7、
，那么的取值范围是
。
3、等腰三角形中，和顶角相邻的外角平分线和底边的位置关系是 。
4、在△ABC中，AB=AC，BD是角平分线，如果∠A＝500，那么∠BDC＝__ __度。
5、等腰三角形有一个角为1160，那么它的底角为__ __度。
6、在△ABC中，AB＝AC，若∠B＝2∠A，则∠C＝___ _度。
7、在△ABC中，AB＝7，AC＝5，则BC边上的中线AD的取值范围是：
8、三角形的三边分别为、
、
且满足
，则这个三角形（按边分类）一定是
三角形。
9、等腰三角形的底边长为10cm，一腰上的中线把这个三角形的周长分为两部分，这两部分之差为4cm，那么这个等腰三角形的腰长是 cm。
10、在△ABC中，AB及AC边的垂直平分线相交于O点，∠A＝800，则∠BOC＝ 度。
二、选择题
1、判定两个等腰三角形全等的条件可以是（ ）。
A、有一腰和一角对应相等 B、有顶角和一个底角对应相等
C、有两边对应相等 D、有两角对应相等
2、在△ABC中，AB=AC，下列推理中错误的是（ ）。
A、如果AD是中线，那么AD⊥BC，∠BAD=∠DAC
B、如果BD是高，那么BD是角平分线
C、如果AD是高，那么∠BAD=∠DAC、BD=DC
D、如果AD是角平分线，那么AD也是BC边的垂直平分线
3、如图，P、Q是△ABC边BC上的两点，且QC＝AP＝AQ＝BP＝PQ，则∠BAC＝（ ）
A、1250 B、1300 C、900 D、1200
3题图 4题图 5题图
4、如图，OP平分∠AOB，PC⊥OA，PD⊥OB，垂足分别是C、D，下列结论错误的是（ ）
A、PC＝PD B、OC＝PC C、∠CPO＝∠DPO D、OC＝OD
5、如图，AB＝DB、∠ABD＝∠CBE，欲证△ABE≌△DBC，则需添加条件不正确的是（ ）
A、∠A＝∠D B、∠E＝∠C C、BC＝BE D、∠A＝∠C
6、三角形的三边分别为、、且满足
，则这个三角形是（ ）
A、等腰直角三角形 B、等边三角形 C、直角三角形 D、等腰三角形
7、使两个直角三角形全等的条件是（ ）
A、两直角边对应相等 B、一锐角对应相等 C、两锐角对应相等 D、斜边相等
8、三角形三个内角的度数分别为
、
、
，（＞
＞0）则该三角形一定有一个角是（ ）
A、600 B、720 C、360 D、450
9、等腰三角形一腰上的高与底边所夹的角等于（ ）。
A、顶角 B、顶角的一半 C、顶角的2倍 D、底角的一半
10、如图：∠1、∠2、∠3、∠4恒满足的关系式是（ ）
A、∠1＋∠2＝∠3＋∠4 B、∠1＋∠2＝∠4－∠3
C、∠1＋∠4＝∠2＋∠3 D、∠1＋∠4＝∠2－∠3
10题图 11题图 12题图
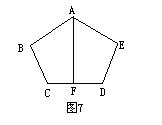
11、如图，△ABC中，AB＝AC，BD、CE为中线，图中共有等腰三角形（ ）个。
A、4个 B、6个 C、3个 D、5个
12、如图△ABC和△CDE都是等边三角形，B、C、D在同一直线上，图中共有（ ）全等三角形。
A、1对 B、 1对 C、 3对 D、4对
13、如图，在△ABC中，AB＝AC，AD＝BD＝BC，则∠C＝（ ）度。
A、720 B、600 C、750 D、450
13题图 14题图 15题图
14、如图，AB＝AC，AE＝EC，∠ACE＝280，则∠B的度数是（ ）
A、600 B、700 C、760 D、450
15、已知：如图，点E在BA的延长线上，EG⊥BC于G，△ADE是等边三角形，那么（ ）
A、∠BAC＝3∠B B、∠BAC＝4∠B C、∠BAC＝2∠B D、∠BAC＝5∠B一、附加题
选择题：
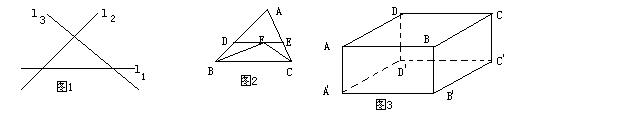
1、如图1，直线l1、l2、l3表示三条相交交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）
A、一处 B、二处 C、三处 D、四处
2、如图2，在△ABC中，∠B、∠C的平分线相交于F，过F作DE∥BC，交AB于D，交AC与E，那么下列结论正确的是（ ）
①△BDF、△CEF都是等腰三角形；②DE=BD+CE；③AD+DE+AE=AB+AC；④BD=CF
A、③④ B、①② C、①②③ D、②③④
3、尺规作图与（ ）公理有密切联系。
A、SAS B、ASA C、SSS D、HL
4、△ABC中，过顶点C作边AB的垂线，将∠C分为50°和20°的两角，则△ABC按角分类是（ ），按边分类是（ ）
A、直角三角形 B、等腰三角形 C、等边三角形 D、斜三角形
三、解答下列各题
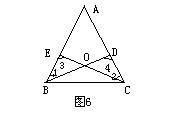
11、如图6，△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O，给出下列四个条件：（1）∠1=∠2，（2）∠3=∠4，（3）BE=CD，（4）OB=OC
（1）上述四个条件中，哪两个条件可判定△ABC是等腰三角形（用序号写出所有情形）
（2）选择第（1）小题中的一种情形，证明△ABC是等腰三角形。
12、如图，AB=AE，∠B=∠E，BC=DE，点F是CD的中点。
（1）求证：AF⊥CD。
（2）在你边结BE后，还有得出什么新的结论，请写出三个（不要求证明）。
13、如图△ACB、△ECD都是等腰直角三角形，且C在AD上，AE的延长线与BD并于F，请你在图中找出一对全等三角形，并写出证明它们全等的过程。
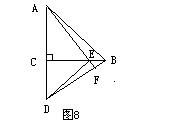
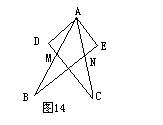
15、如图14，在△ABE和△ACD中，给出以下四个论断：
（1）AB=AC；（2）AD=AE；（3）AM=AN；（4）AD⊥DC、AE⊥BE，以其中三个论断为题设，填入下面的“已知”栏中，一个论断为结论，填入下面的“求证”栏中，使之组成一个真命题，并写出证明过程。
已知：如图14，在△ABE和△ACD中
求证：
证明：
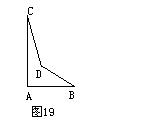
18、一个零件的形状如图19，按规定∠A=90°，∠C=21°，∠C=21°，检验以量得∠BDC=148°，就判定这个零件不合格，运用三角形的有关知识说明零件不合格的理由。
