初二数学联考试卷
命题:李亮 制卷:李亮 总分:120分 时间:120分钟
一、填空题(3’×10=30’)
1、已知△ABC≌△DEF,∠A=60°,∠B=70°,AB=20㎝,则∠C’ =_____度,A’B’ =_____㎝。
2、已知△ABC≌△DEF,且△ABC的周长为12㎝,面积为6㎝2,则△DEF的周长为__________,面积为__________。
3、如图一,已知AB=CD,若根据“SSS”证得△ABC≌△CDA,需要添加的一个条件是__________。
4、如图二,AC和BD相交于点O,且AO=CO,BO=DO,则图中共有全等三角形共有_____对。
5、如图三,点A在BE上,AD=AE,AB=AC,∠1=∠2=30°,则∠3的度数为_____。
6、如图四,△ABC中,AD⊥BC于D,BE⊥AC于E,AD和BE相交于点F,若BF=AC,则∠ABC=_____度。
7、全等三角形的对应边_____,对应角_____。
8、如图五,已知AB=DE,,BC=EF,请再写出一个条件__________,使三角形△ABC≌△DEF。
9、如图六,AB=AC,EB=EC,AE的延长线交BC于D,那么图中的全等三角形共有_____对。
10、证明两个三角形全等的方法共有_____种。
二、选择题(3’×10=30’ )
1、下列命题是假命题的是( )
A、有斜边和一个锐角对应相等的两个直角三角形全等;
B、有一条直角边和一个锐角对应相等的两个直角三角形全等;
C、有两角和一边对应相等的两个三角形全等;
D、有两边和其中一边的对角对应相等的两个三角形全等。
2、不能推出两个三角形全等的条件是( )
A、有两边和夹角对应相等 B、有两角和夹边对应相等
C、有两角和一边对应相等 D、有两边和一角对应相等
3、下列说法:①、全等三角形的形状相同,大小相等;②、全等三角形的对应边相等;③、全等三角形的对应角相等;④、全等三角形的周长、面积分别相等;⑤、所有的正方形都是全等形、所有的等边三角形都是全等形。其中正确的说法有:( )
A、5个 B、4个 C、3个 D、2个
4、根据下列条件,不能画出唯一三角形的是( )
A、已知三边 B、已知两边和夹角
C、已知两角和夹边 D、已知两边及其中一边的对角
5、如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形第三边所对的角的关系是( )
A、相等 B、不相等 C、互余 D、互补或相等
6、如图七,在△ABC中,AB=AC,D为BC的中点,
那么以下结论不正确的是( )
A、△ABC≌△ACD B、∠B=∠C
C、AD是△ABC的角平分结 D、AD不是△ABC的高
7、下列说法:①、两条直角边对应相等的两个直角三角形全等;②、腰和顶角对应相等的两个等腰三角形全等;③、腰长相等且有一个角是85°的两个等腰三角形全等;④、腰长相等且有一个角是100°的两个等腰三角形全等;⑤、两边和一角对应相等的两个三角形全等;⑥、等腰三角形顶角的平分线把这个等腰三角形分成的两个三角形全等。其中正确的说法有( )
A、3个 B、4个 C、5个 D、6个
8、如图八,OP平分∠AOB,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
A、PC=PD B、OC=OD
C、∠OPC=∠OPD D、OC>PC
9、如图九,点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2=∠3,AC=AE,则( )
A、△AEF≌△ACD B、△ABD≌△AFE
C、△ADC≌△AFE D、△ABC≌△ADE
10、已知,如图十,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD。有下列结论:①、AD=BC,;∠DBC=∠CAD;③、AO=BO;④、AB∥CD。其中正确的是( )
A、①②③④ B、①②③
C、①②④ D、②③④
三、解答、证明题(8’×5=40’)
1、已知:点E、F在BC上,BF=CE,AB=DC,AE=DF。
求证:∠A=∠D。
2、已知:AE=AC,AB=AD,∠EAB=∠CAD。
求证:∠B=∠D。
3、已知:在四边形ABCD中,E是AC上一点,∠1=∠2,∠3=∠4。
求证:∠5=∠6。
4、已知:AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD。
求证:BE⊥AC。
5、已知:∠1=∠2,∠3=∠4。
求证:CE=DE。
四、附加题(10’×2=20’)
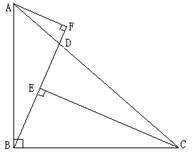
1、已知:∠ABC=90°,AB=BC,D为AC上一点,CE⊥BD于E,AF⊥直线BD于F。
求证:EF=CE—AF。
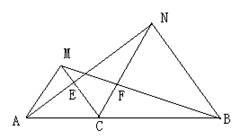
2、已知:点C为线段AB上一点,△ACM和△CBN是等边三角形。
求证:(1)、AN=BM;
(2)、△ACE≌△MCF。